| | Images fractales |  |
|
|
|
| Auteur | Message |
|---|
Yannick
Nombre de messages : 8635
Age : 53
Localisation : Bretagne
Date d'inscription : 15/02/2010
 |  Sujet: re Sujet: re  Dim 19 Jan 2014 - 16:06 Dim 19 Jan 2014 - 16:06 | |
| On dirait les deux hémisphères d' un cerveau mais je serai inquiet que ce soit le mien...  euh...le premier... | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Sam 1 Mar 2014 - 9:18 Sam 1 Mar 2014 - 9:18 | |
| | |
|
  | |
Yannick
Nombre de messages : 8635
Age : 53
Localisation : Bretagne
Date d'inscription : 15/02/2010
 |  Sujet: re Sujet: re  Sam 1 Mar 2014 - 12:43 Sam 1 Mar 2014 - 12:43 | |
| | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Dim 1 Juin 2014 - 10:56 Dim 1 Juin 2014 - 10:56 | |
| En relation avec le programme que j'ai récemment proposé sur les fractales de Newton, voici les images correspondant aux équations z^n - 1 = 0 pour différentes valeurs de n, indiquées sur la figure. L'équation possède n racines complexes, situées au niveau des points verts sur les figures. Les bassins d'attraction de chaque racine sont représentés par les bandes bleu-vert. La frontière (fractale) entre les différents bassins est représentée en rouge. Cette frontière devient de plus en plus complexe à mesure que l'exposant augmente. J'ai fait ces images avec un programme en FreeBASIC, mais je pense pouvoir y arriver avec PANORAMIC lorsque j'aurai réglé les problèmes de SUBs. 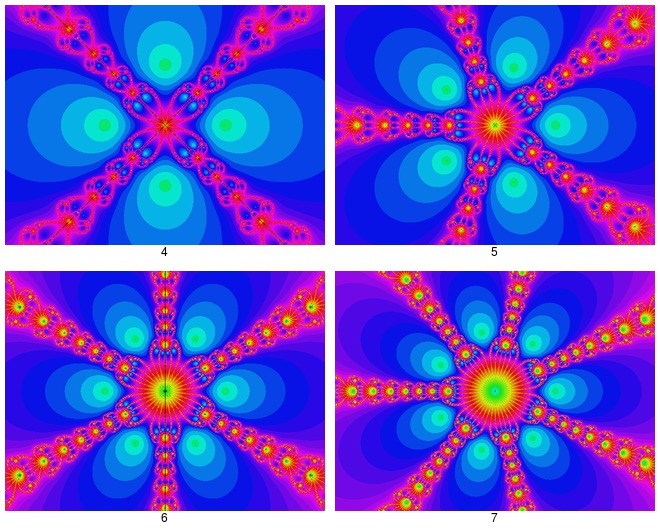 | |
|
  | |
Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Dim 1 Juin 2014 - 23:34 Dim 1 Juin 2014 - 23:34 | |
| Bon courage Jean. En tout cas, c'est très beau. | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Mar 3 Juin 2014 - 9:04 Mar 3 Juin 2014 - 9:04 | |
| Merci Jicehel  Voici un autre exemple montrant ce qui se passe lorsqu'on augmente progressivement l'exposant p dans l'équation z^p - 1 = 0, en partant d'un entier impair (ici 3). La frontière fractale du côté des x négatifs s'élargit considérablement, et pour les plus fortes valeurs de l'exposant (ici 3,9) il y a des points (en noir sur l'image) pour lesquels la suite ne converge pas. Tout cela sera expliqué plus en détail dans l'article en cours. 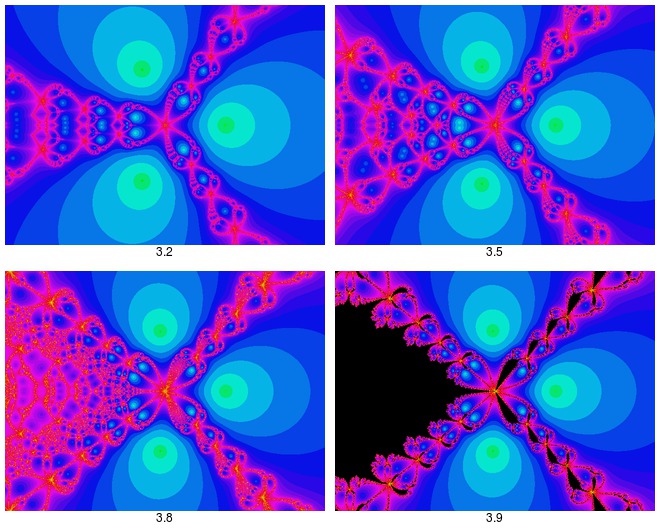 | |
|
  | |
papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Mar 3 Juin 2014 - 12:02 Mar 3 Juin 2014 - 12:02 | |
| Rien que du beau!
Merci Jean_Debord. | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Mer 4 Juin 2014 - 8:55 Mer 4 Juin 2014 - 8:55 | |
| Merci Papydall  Voici un autre exemple, cette fois-ci en partant d'un exposant pair. On voit apparaître sur la gauche de l'image (du côté des x négatifs) 2 racines qui s'écartent progressivement l'une de l'autre à mesure que l'exposant augmente. Dans le même temps la frontière fractale entre ces 2 racines se constitue progressivement à partir d'une "émanation" issue du "noyau" central. 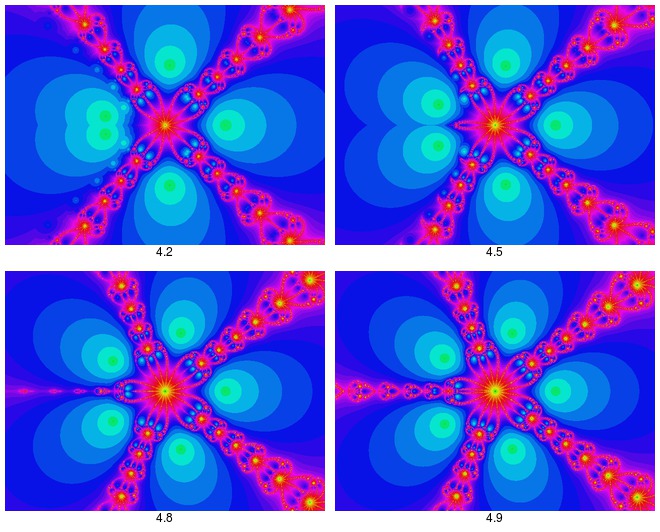 | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Jeu 5 Juin 2014 - 9:05 Jeu 5 Juin 2014 - 9:05 | |
| Dernier exemple avant de soumettre mon article : cette fois-ci avec un exposant complexe : z^p - 1 avec p = 3(1+yi), où y varie de 0 à 1. La valeur de y est indiquée sur les images. On constate une discontinuité sur l'axe des x négatifs ainsi qu'une distortion de la frontière fractale qui devient de plus en plus "complexe". 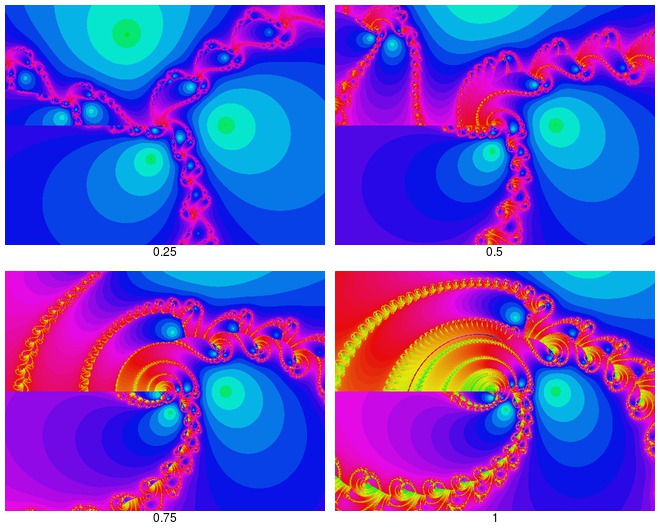 L'article contiendra tous ces exemples + 2 autres concernant les fonctions trigonométriques et exponentielles. | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Lun 16 Juin 2014 - 9:13 Lun 16 Juin 2014 - 9:13 | |
| Retour aux ensembles de Mandelbrot avec cette image générée par la fonction c[(z+2)^6+(z+2)^(-6)]. On voit apparaître un réseau de filaments formant des structures géométriques très régulières.  | |
|
  | |
papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Lun 16 Juin 2014 - 12:31 Lun 16 Juin 2014 - 12:31 | |
| Ces ensembles de Mandelbrot ne finiront jamais de nous surprendre, et c’est tant mieux !
Je plains ceux qui ne voient pas la beauté de ces images ! | |
|
  | |
Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Lun 16 Juin 2014 - 14:28 Lun 16 Juin 2014 - 14:28 | |
| C'est clair que c'est magnifique.
| |
|
  | |
JL35
Nombre de messages : 7112
Localisation : 77
Date d'inscription : 29/11/2007
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Lun 16 Juin 2014 - 16:57 Lun 16 Juin 2014 - 16:57 | |
| Et même époustouflant ! Ça fait un peu extraterrestre...  | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Mer 18 Juin 2014 - 9:04 Mer 18 Juin 2014 - 9:04 | |
| En pivotant celle-ci vous verrez une sorte de Mickey fractal (avec plusieurs bras, donc probablement d'origine extra-terrestre lui aussi  ) 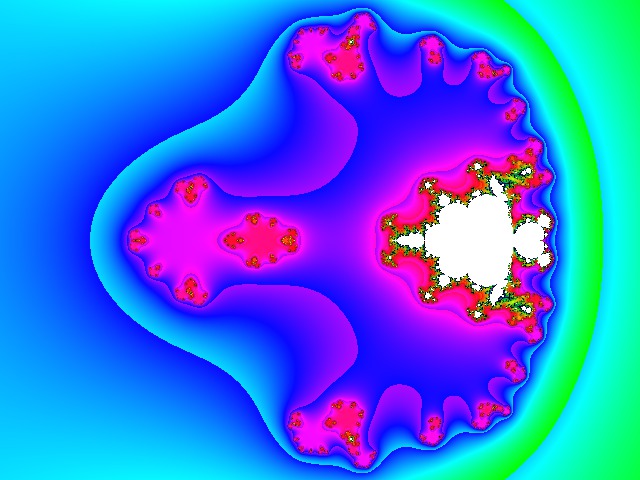 Formule utilisée : [c(z^3 - z^2) - 1]^3 L'image globale se compose de plusieurs parties. Ici j'ai juste agrandi la principale. | |
|
  | |
JL35
Nombre de messages : 7112
Localisation : 77
Date d'inscription : 29/11/2007
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Mer 18 Juin 2014 - 9:40 Mer 18 Juin 2014 - 9:40 | |
| C'est vrai qu'en pivotant ça fait marcher l'imagination  j'y vois une espèce de madone d'un autre monde couvant le feu sacré... Dans tous les cas, c'est magnifique ! | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Jeu 19 Juin 2014 - 9:13 Jeu 19 Juin 2014 - 9:13 | |
| Bien vu, JL35  Mon interprétation était moins poétique  Quoi qu'il en soit, pour trouver des extraterrestres il faut aller vers les étoiles... Aussi, voici une étoile fractale générée par la fonction [c(z^6 - z^5) - 1]^2 : 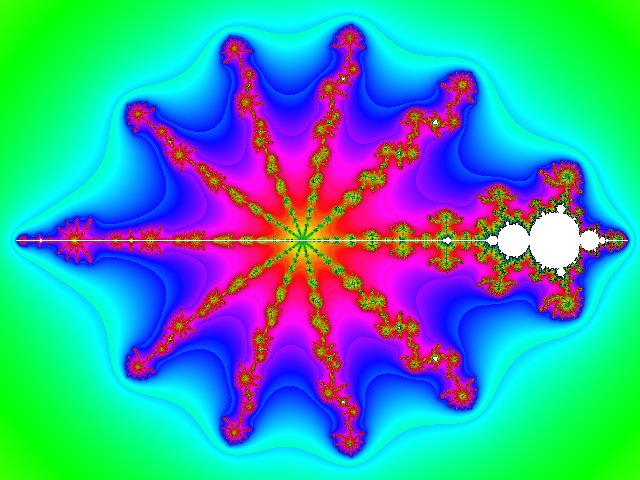 Ici, l'antenne de l'ensemble de Mandelbrot (prolongement rectiligne à l'ouest de l'ensemble) a subi une expansion considérable, générant une formation étoilée de taille importante par rapport à l'ensemble proprement dit (en blanc). | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Dim 22 Juin 2014 - 19:24 Dim 22 Juin 2014 - 19:24 | |
| Voici l'effet obtenu en augmentant l'exposant p dans la formule {c[z^p - z^(p-1)] - 1}^2 : l'étoile a de plus en plus de branches qui s'étendent de plus en plus loin dans l'espace. 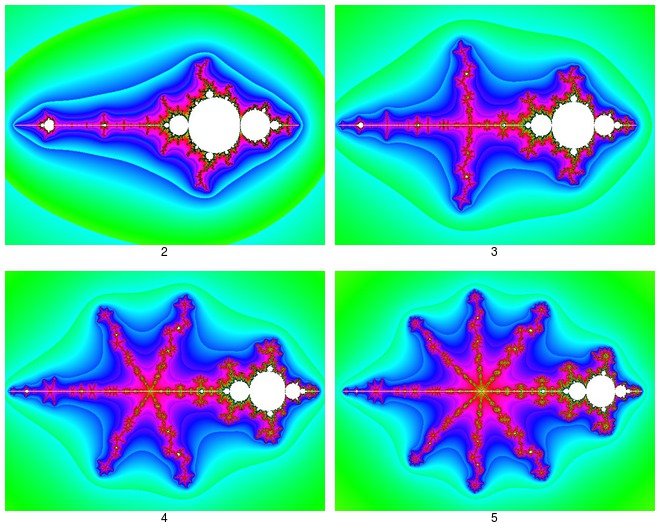 Les images sont désignées par les valeurs de p. L'échelle est ajustée pour compenser l'extension des branches. Le cas p = 6 a été présenté dans le message précédent. | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Sam 28 Juin 2014 - 10:12 Sam 28 Juin 2014 - 10:12 | |
| Deux autres exemples avec les exposants 10 et 15. Ici l'étoile prend toute la place. L'ensemble de Mandelbrot est réduit à la portion congrue. 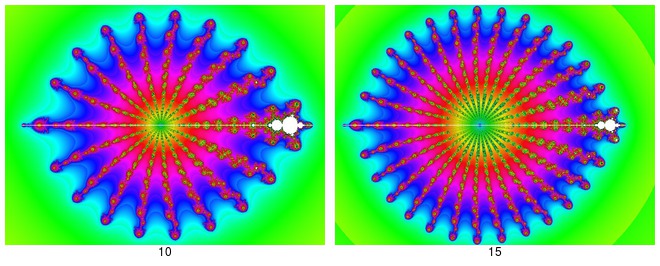 Pour les exposants au-delà de 15, la méthode de coloration que j'utilise semble prise en défaut : il apparaît des bandes noires, du plus mauvais effet. Donc je ne les montre pas ! | |
|
  | |
Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Sam 28 Juin 2014 - 14:21 Sam 28 Juin 2014 - 14:21 | |
| Pas encore en tout cas. Tu trouveras sans doute une astuce qui corrige cette "faille" si l'on peut dire car de toute façon en principe, on donne souvent une plage pour laquelle le programme fonctionne. | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Jeu 25 Sep 2014 - 9:27 Jeu 25 Sep 2014 - 9:27 | |
| Oui j'ai à peu près résolu le problème et j'en profite pour donner l'image correspondant à p=20. C'est une sacrée étoile ! Combien comptez-vous de branches ? 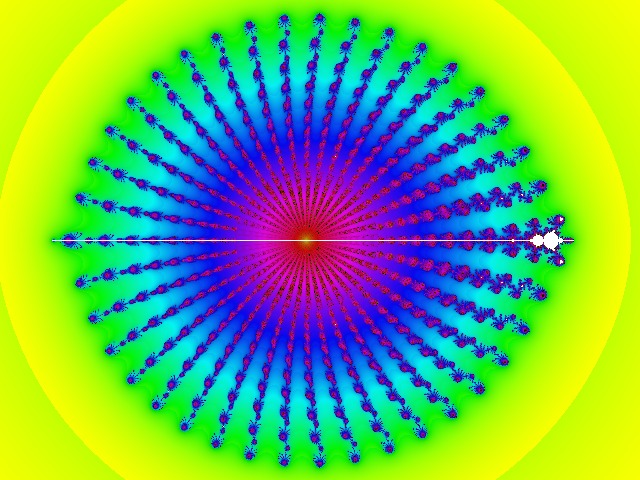 | |
|
  | |
Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Jeu 25 Sep 2014 - 13:38 Jeu 25 Sep 2014 - 13:38 | |
| 39 "grosses branches", les petites étant trop nombreuses | |
|
  | |
papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Ven 26 Sep 2014 - 0:25 Ven 26 Sep 2014 - 0:25 | |
| Voila, au moins un qui sait compter et conter !  J’ai pris connaissance de la présence de ces superbes figures, il y a très longtemps et je suis toujours émerveillé devant ces objets mathématiques tout autant (et même plus) ! Je me suis remis à redécouvrir ces êtres mathématiques qui vivent dans le plan complexe. Je posterai mon code, un de ces jours. En attendant, admirez … | |
|
  | |
Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Ven 26 Sep 2014 - 8:12 Ven 26 Sep 2014 - 8:12 | |
| Oui, elles sont très chouettes, j'avoue  | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Ven 26 Sep 2014 - 9:03 Ven 26 Sep 2014 - 9:03 | |
| - Jicehel a écrit:
- 39 "grosses branches", les petites étant trop nombreuses
Bizarre... Moi j'en compte 38 ! 18 de chaque côté de l'axe Ox ; si l'on compte 2 branches horizontales cela fait 38. D'une façon générale : 2(p-1) où p est l'exposant de la formule [c(z^p - z^q) - 1]^2 avec q = 1 - p En attendant qu'on se mette d'accord, voici un agrandissement d'une expansion située sur l'un de ces ensembles :  | |
|
  | |
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  Ven 26 Sep 2014 - 9:10 Ven 26 Sep 2014 - 9:10 | |
| - papydall a écrit:
- Je posterai mon code, un de ces jours.
Je suppose que tu as adapté les programmes donnés sur cette page : http://www.madteddy.com/biomorph.htmJe m'en suis moi-même inspiré pour mon article sur les biomorphes de Pickover. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Images fractales Sujet: Re: Images fractales  | |
| |
|
  | |
| | Images fractales |  |
|
