| Novembre 2024 | | Lun | Mar | Mer | Jeu | Ven | Sam | Dim |
|---|
| | | | | 1 | 2 | 3 | | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | 11 | 12 | 13 | 14 | 15 | 16 | 17 | | 18 | 19 | 20 | 21 | 22 | 23 | 24 | | 25 | 26 | 27 | 28 | 29 | 30 | |  Calendrier Calendrier |
|
|
| | Les Courbes de Bézier cubiques |  |
|
+4Minibug jean_debord Marc papydall 8 participants | | Auteur | Message |
|---|
papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Les Courbes de Bézier cubiques Sujet: Les Courbes de Bézier cubiques  Ven 30 Mar 2018 - 5:02 Ven 30 Mar 2018 - 5:02 | |
| - Code:
-
rem ============================================================================
rem Les Courbes de Bézier cubiques
rem Par Papydall le 30/03/2018
rem ============================================================================
rem REF : https://fr.wikipedia.org/wiki/Courbe_de_B%C3%A9zier
rem ============================================================================
rem Une courbe de Bézier cubique est définie par quatres points P0, P1, P2 et P3
rem de coordonnées (x0,y0), (x1,y1), (x2,y2) et (x3,y3)
rem P0 et P3 correspondent aux points des extrémités ou nœuds de la courbe.
rem P1 et P2 correspondent aux points de contrôle ou poignées, chacun apparié
rem avec l’un des points terminaux.
rem Les points de contrôle ont l’utile propriété suivante :
rem Une ligne commençant à une extrémité de la courbe et se terminant au point de
rem contrôle correspondant est tangente à la courbe au point terminal.
rem Ceci permet la jonction douce de multiples courbes de Bézier.
rem La courbe se trace en partant du point P0, en se dirigeant vers le point P1
rem et en arrivant au point P3 selon la direction P2-P3.
rem La courbe ne passe pas nécessairement par P1 ni par P2.
rem ============================================================================
rem L’équation paramétrique de la courbe de bézier cubique est :
rem ______________________________________________________________________
rem | |
rem | x(t) = (1-t)³x0 + 3t(1-t)²x1 + 3t²(1-t)x2 + t³x3 pour 0 <= t <= 1 |
rem | y(t) = (1-t)³y0 + 3t(1-t)²y1 + 3t²(1-t)y2 + t³y3 pour 0 <= t <= 1 |
rem |______________________________________________________________________|
rem ============================================================================
' ------------------------------------------------------------------------------
' Les courbes de Bézier sont utilisées en conception graphique
' ------------------------------------------------------------------------------
rem ============================================================================
dim xc,yc,p
picture 10 : full_space 10 : 2d_target_is 10 : print_target_is 10 : color 10,0,0,0
font_color 10, 255,255,255 : 2d_pen_color 255,000,000 : font_bold 10
font_name 10,"arial" : font_size 10,14 : 2d_fill_off
xc = width_client(10)/2 : yc = height_client(10)/2 : p = 1000 : ' pause pour suivre le tracé
' Exemples des courbes de Bézier
caption 0,"Exemples des courbes de Bézier"
2d_pen_color 255,000,000 : Cubic_Bezier_Curve(120,20,20,100,200,100,320,20) : pause p : color 10,0,0,0
2d_pen_color 255,255,000 : Cubic_Bezier_Curve(300,200,200,100,400,200,350,100) : pause p : color 10,0,0,0
2d_pen_color 000,255,000 : Cubic_Bezier_Curve(100,400,200,200,300,400,550,220) : pause p : color 10,0,0,0
2d_pen_color 000,255,255 : Cubic_Bezier_Curve(100,350,500,50,80,50,400,250) : pause p : color 10,0,0,0
2d_pen_color 255,000,255 : Cubic_Bezier_Curve(100,400,200,200,400,220,450,350) : pause p : color 10,0,0,0
2d_pen_color 255,255,255 : Cubic_Bezier_Curve(114,165,208,444,360,165,114,165) : pause p : color 10,0,0,0
' Dessiner différentes figures avec les courbes de Bézier
caption 0,"Tracé d'une Soucoupe par les courbes de Bézier" : Soucoupe() : pause p
caption 0,"Tracé d'un Coeur par les courbes de Bézier" : Coeur() : pause p
caption 0,"Tracé d'une Fleur par les courbes de Bézier" : Fleur() : pause p
caption 0,"Tracé d'un Oeuf par les courbes de Bézier" : Oeuf() : pause p
caption 0,"Tracé d'une pièce d'un Puzzle par les courbes de Bézier" : Puzzle() : pause p
caption 0,"Tracé d'un vase par les courbes de Bézier" : Vase() : pause p
caption 0,"Tracé d'une voiture par les courbes de Bézier" : Voiture() : pause p
caption 0,"Tracé d'une bulle de dialogue par les courbes de Bézier" : Bulle_De_Dialogue() : pause p
caption 0,"Tracé de pacman par les courbes de Bézier" : Pacman() : pause p
2d_pen_color 255,255,0 : color 10,0,0,0 : font_color 10,200,100,20 : 2d_fill_off
caption 0,"Tracé d'un rectangle avec coins arrondis par les courbes de Bézier"
Rectangle_Arrondi(100,300,200,100,50)
print_target_is 10 : font_size 10,16 : print_locate 120,340 : print "That's All folks !!"
end
rem ============================================================================
rem &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
rem ============================================================================
' Fonction retournant le cube de son argument
FNC Cube(n)
result n*n*n
END_FNC
rem ============================================================================
' Fonction retournant le carré de son argument
FNC Carre(n)
result n*n
END_FNC
rem ============================================================================
' Dessiner un arc de cercle centré à la position (x, y), de rayon r, commençant
' à angleInitial (en degré) et finissant à angleFinal (en degré) en allant dans
' le sens indiqué par s (s = 0 : sens horaire ; s = 1 : sens trigonométrique).
SUB Arc(x,y,r,aInitial,aFinal,s)
dim_local a,a1,a2
degrees
if s > 0
a1 = aInitial : a2 = aFinal
else
a1 = aFinal : a2 = 360+aInitial
end_if
2d_poly_from x+r*cos(a1),y-r*sin(a1)
for a = a1 to a2
2d_poly_to x+r*cos(a),y-r*sin(a)
next a
END_SUB
rem ============================================================================
' Tracé d'une courbe de Bézier cubique (de degré 3)
SUB Cubic_Bezier_Curve(x0,y0,x1,y1,x2,y2,x3,y3)
dim_local np
np = 100 : ' nombre de points interpolés sur la courbe,
' plus ce nombre est grand, plus la courbe sera lisse
dim_local bezier(np,2) : ' Tableau des coordonnées des points de la courbe
dim_local i,t,xp0,xp1,xp2,xp3,yp0,yp1,yp2,yp3
2d_poly_from x0,y0 : ' Point de départ du tracé
for i = 0 to np
t = i/np : ' t varie entre 0.0 et 1.0
xp0 = Cube(1-t)*x0 : yp0 = Cube(1-t)*y0
xp1 = 3*Carre(1-t)*t*x1 : yp1 = 3*Carre(1-t)*t*y1
xp2 = 3*(1-t)*Carre(t)*x2 : yp2 = 3*(1-t)*Carre(t)*y2
xp3 = Cube(t)*x3 : yp3 = Cube(t)*y3
bezier(i,0) = xp0 + xp1 + xp2 + xp3 : ' Coordonnées x(t)
bezier(i,1) = yp0 + yp1 + yp2 + yp3 : ' Coordonnées y(t)
2d_poly_to bezier(i,0),bezier(i,1) : ' Relier la courbe au point (x(t),y(t))
display
next i
' Activer la ligne suivante pour voir les points définissant la courbe
' 2d_circle x0,y0,2 : 2d_circle x1,y1,2 : 2d_circle x2,y2,2 : 2d_circle x3,y3,2
END_SUB
rem ============================================================================
' Dessiner une soucoupe avec les courbes de Bézier
SUB Soucoupe()
' Le bas de la soucoupe
2d_pen_color 220,100,0
Cubic_Bezier_Curve(284,169,284,197,229,220,160,220) :' pause p
Cubic_Bezier_Curve(160,220,91,220,36,197,36,169) :' pause p
Cubic_Bezier_Curve(36,169,36,141,91,118,160,118) :' pause p
Cubic_Bezier_Curve(160,118,229,118,284,141,284,169) :' pause p
2d_flood 220,200,220,100,0
' Le haut de la soucoupe
2d_pen_color 50,190,0
Cubic_Bezier_Curve(223,120,223,133,194,143,159,143) :' pause p
Cubic_Bezier_Curve(159,143,124, 143, 96, 133, 96, 120) :' pause p
Cubic_Bezier_Curve(96,129,96, 108, 124, 97, 159, 97) :' pause p
Cubic_Bezier_Curve(159,97,194, 97, 223, 108, 223, 120) :' pause p
2d_flood 140,128,50,190,0 : 2d_flood 162,108,51,190,0
END_SUB
rem ============================================================================
SUB Coeur()
label dcoeur
dim_local x1,y1,x2,y2,x3,y3,x4,y4
dim_local i,p
p = 1000
2d_pen_color 255,0,0 : color 10,0,0,0
restore_label dcoeur
read x1 : read y1 : x1 = xc+x1 : y1 = yc+y1
for i = 1 to 4
read x2 : read y2 : read x3 : read y3 : read x4 : read y4
x2 = xc+x2 : y2 = yc+y2 : x3 = xc+x3 : y3 = yc+y3 : x4 = xc+x4 : y4 = yc+y4
Cubic_Bezier_Curve(x1,y1,x2,y2,x3,y3,x4,y4) : ' pause p
x1 = x4 : y1 = y4
next i
END_SUB
rem ============================================================================
SUB Fleur()
label dfleur
dim_local x1,y1,x2,y2,x3,y3,x4,y4
dim_local i
2d_pen_color 255,0,0 : color 10,0,0,0
restore_label dfleur
read x1 : read y1 : x1 = xc+x1 : y1 = yc+y1
for i = 1 to 12
read x2 : read y2 : read x3 : read y3 : read x4 : read y4
x2 = xc+x2 : y2 = yc+y2 : x3 = xc+x3 : y3 = yc+y3 : x4 = xc+x4 : y4 = yc+y4
Cubic_Bezier_Curve(x1,y1,x2,y2,x3,y3,x4,y4) :' pause p
x1 = x4 : y1 = y4
next i
END_SUB
rem ============================================================================
SUB Oeuf()
label dOeuf
dim_local x1,y1,x2,y2,x3,y3,x4,y4
dim_local i
2d_pen_color 255,0,0 : color 10,0,0,0
restore_label dOeuf
read x1 : read y1 : x1 = xc+x1 : y1 = yc+y1
for i = 1 to 4
read x2 : read y2 : read x3 : read y3 : read x4 : read y4
x2 = xc+x2 : y2 = yc+y2 : x3 = xc+x3 : y3 = yc+y3 : x4 = xc+x4 : y4 = yc+y4
Cubic_Bezier_Curve(x1,y1,x2,y2,x3,y3,x4,y4) : ' pause p
x1 = x4 : y1 = y4
next i
END_SUB
rem ============================================================================
SUB Puzzle()
label dPuzzle
dim_local x1,y1,x2,y2,x3,y3,x4,y4
dim_local i
2d_pen_color 255,0,0 : color 10,0,0,0
restore_label dPuzzle
read x1 : read y1 : x1 = xc+x1 : y1 = yc+y1
for i = 1 to 16
read x2 : read y2 : read x3 : read y3 : read x4 : read y4
x2 = xc+x2 : y2 = yc+y2 : x3 = xc+x3 : y3 = yc+y3 : x4 = xc+x4 : y4 = yc+y4
Cubic_Bezier_Curve(x1,y1,x2,y2,x3,y3,x4,y4) :' pause p
x1 = x4 : y1 = y4
next i
END_SUB
rem ============================================================================
SUB Vase()
label dVase
dim_local x1,y1,x2,y2,x3,y3,x4,y4
dim_local i
2d_pen_color 255,0,0 : color 10,0,0,0
restore_label dVase
read x1 : read y1 : x1 = xc+x1 : y1 = yc+y1
for i = 1 to 6
read x2 : read y2 : read x3 : read y3 : read x4 : read y4
x2 = xc+x2 : y2 = yc+y2 : x3 = xc+x3 : y3 = yc+y3 : x4 = xc+x4 : y4 = yc+y4
Cubic_Bezier_Curve(x1,y1,x2,y2,x3,y3,x4,y4) : ' pause p
x1 = x4 : y1 = y4
next i
END_SUB
rem ============================================================================
SUB Voiture()
label dVoiture
dim_local x1,y1,x2,y2,x3,y3,x4,y4
dim_local i
2d_pen_color 255,0,0 : color 10,0,0,0
restore_label dVoiture
read x1 : read y1 : x1 = xc+x1 : y1 = yc+y1
for i = 1 to 3
read x2 : read y2 : read x3 : read y3 : read x4 : read y4
x2 = xc+x2 : y2 = yc+y2 : x3 = xc+x3 : y3 = yc+y3 : x4 = xc+x4 : y4 = yc+y4
Cubic_Bezier_Curve(x1,y1,x2,y2,x3,y3,x4,y4) : ' pause p
x1 = x4 : y1 = y4
next i
END_SUB
rem ============================================================================
SUB Bulle_De_Dialogue()
2d_pen_color 255,0,0 : color 10,0,0,0 : 2d_fill_off : font_color 10,200,100,20
Cubic_Bezier_Curve(75,25,25,25,25,25,25,62)
Cubic_Bezier_Curve(25,62,25,100,25,100,50,100)
Cubic_Bezier_Curve(50,100,50,120,50,120,30,125)
Cubic_Bezier_Curve(30,125,60,120,60,120,65,100)
Cubic_Bezier_Curve(65,100,125,100,125,100,125,62)
Cubic_Bezier_Curve(125,62,125,25,125,25,75,25)
print_locate 50,50 : print "Salut !"
END_SUB
rem ============================================================================
' Tracer un rectangle avec coins arrondis
SUB Rectangle_Arrondi(x,y,largeur,hauteur,rayon)
2d_line x,y+rayon,x,y+hauteur-rayon
Cubic_Bezier_Curve(x,y+hauteur-rayon,x,y+hauteur,x,y+hauteur,x+rayon,y+hauteur)
2d_poly_to x+largeur-rayon,y+hauteur
Cubic_Bezier_Curve(x+largeur-rayon,y+hauteur,x+largeur,y+hauteur,x+largeur,y+hauteur,x+largeur,y+hauteur-rayon)
2d_poly_to x+largeur,y+rayon
Cubic_Bezier_Curve(x+largeur,y+rayon,x+largeur,y,x+largeur,y,x+largeur-rayon,y)
2d_poly_to x+rayon,y
Cubic_Bezier_Curve(x+rayon,y,x,y,x,y,x,y+rayon)
END_SUB
rem ============================================================================
SUB Pacman()
dim_local i
2d_pen_color 255,0,0 : color 10,0,0,0
Rectangle_Arrondi(12,12,150,150,15)
Rectangle_Arrondi(19,19,150,150, 9)
Rectangle_Arrondi(53,53,49,33,10)
Rectangle_Arrondi(53,119,49,16,6)
Rectangle_Arrondi(135,53,49,33,10)
Rectangle_Arrondi(135,119,25,49,10)
Arc(37,37,13,-180/7,180/7,0)
2d_poly_to 31,37 : 2d_poly_to 37+13*cos(180/7),37-13*sin(180/7)
2d_flood 29,37,255,0,0
2d_fill_color 255,0,0
for i = 0 to 7 : 2d_rectangle 51+i*16,35,55+i*16,39 : next i
for i = 0 to 5 : 2d_rectangle 115,51+i*16,119,55+i*16 : next i
for i = 0 to 7 : 2d_rectangle 51+i*16,99,55+i*16,103 : next i
2d_line 83,116,83,102
Cubic_Bezier_Curve(83,102,83,94,89,88,97,88)
Cubic_Bezier_Curve(97,88,105,88,111,94,111,102)
2d_poly_to 111,116 : 2d_poly_to 106,111 : 2d_poly_to 102,116
2d_poly_to 92,116 : 2d_poly_to 88,111 : 2d_poly_to 83,116
2d_flood 100,110,255,0,0
2d_pen_color 0,0,0 : 2d_fill_color 0,0,0
2d_circle 101,102,2 : 2d_circle 89,102,2
END_SUB
rem ============================================================================
' Coeur 12 points
dCoeur:
data 1, -70, 82,-162, 162, -82, 123, -1
data 97, 51, 51, 51, 0, 160, -51, 51
data -97, 51, -133,-1, -162, -82, -82, -162
data 1, -70
rem ============================================================================
' Fleur 36 points
dFleur:
data 2, 172,-252, -75,217, -41,-85, 150
data -183, -188,208, 75,-148, 88,-62, -255
data 144, 168,-172, 2,75, -252,38, 218
data -150, -85,189, -182,-75, 208,-88, -148
data 255, -62,-168, 144,-2, -172,252, 75
data -218, 38, 85, -150, 179, 192, -207, -76
data 148, -88, 62, 255, -143, -169, 172, -2
data -75, 252, -41, -217, 150, 85, -189, 182
data 75, -208, 88, 148, -255, 62, 169, -143
data 2, 172
rem ============================================================================
' Oeuf 12 points
dOeuf:
data 0, -150, 76, -151, 114, -101, 115, -26
data 114, 75, 56, 149, 0, 152, -56, 149
data -114, 75, -115, -26, -114, -101, -76, -151
data 0, -150
rem ============================================================================
' Puzzle 48 points
dPuzzle:
data 1, -68, 48, -70, 64, -92, 47, -151
data 45, -152, 149, -151, 149, -151, 151, -148
data 150, -57, 149, -40, 169, -39, 227, -79
data 235, 0, 227, 76, 160, 34, 149, 40
data 148, 43, 149, 150, 149, 149, 149, 148
data 37, 149, 39, 149, 36, 147, 89, 73
data 2, 60, -44, 66, -60, 80, -36, 150
data -39, 149, -150, 151, -149, 149, -151, 148
data -150, 36, -149, 35, -138, 41, -68, 58
data -62, -2, -73, -84, -144, -38, -149, -42
data -150, -43, -149, -150, -149, -149, -149, -148
data -43, -149, -43, -150, -44, -151, -77, -72
data 1, -68
rem ============================================================================
dvase:
data -20,-80, -10,-60, -10,-60, -20,-40
data -50, 20, -50, 20, -20, 80
data -20, 80, 20, 80, 20, 80
data 50, 20, 50, 20, 20,-40
data 10,-60, 10,-60, 20,-80
data 00,-80, 00,-80, -20,-80
rem ============================================================================
dVoiture:
data 40,100
data 40,75,50,75,90,70
data 95,60,95,60,95,50
data 180,40,180,70,190,100
rem ============================================================================
| |
|   | | Marc

Nombre de messages : 2466
Age : 63
Localisation : TOURS (37)
Date d'inscription : 17/03/2014
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Ven 30 Mar 2018 - 16:45 Ven 30 Mar 2018 - 16:45 | |
| Merci Papydall !
C'est super bien fait !
Quant au PacMan : très réussi et réaliste !
Et le code source.... le Code source .... extra ! | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Sam 31 Mar 2018 - 1:07 Sam 31 Mar 2018 - 1:07 | |
| Merci Marc.
De tels retours, c’est bon pour le moral !
| |
|   | | jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Sam 31 Mar 2018 - 9:00 Sam 31 Mar 2018 - 9:00 | |
| Merci Papydall ! Encore un bon exemple à adapter pour FBPano  | |
|   | | Minibug

Nombre de messages : 4570
Age : 58
Localisation : Vienne (86)
Date d'inscription : 09/02/2012
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Sam 31 Mar 2018 - 9:19 Sam 31 Mar 2018 - 9:19 | |
| Très sympa cette présentation sur les courbes de Bézier et très intéressante aussi. Encore une belle démonstration signée Papydall. Félicitation pour ton travail !  | |
|   | | silverman

Nombre de messages : 970
Age : 52
Localisation : Picardie
Date d'inscription : 18/03/2015
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Sam 31 Mar 2018 - 11:01 Sam 31 Mar 2018 - 11:01 | |
| En effet, belle démonstration des courbes de bézier papydall! | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Sam 31 Mar 2018 - 12:19 Sam 31 Mar 2018 - 12:19 | |
| Merci à vous tous.  | |
|   | | Klaus

Nombre de messages : 12331
Age : 75
Localisation : Ile de France
Date d'inscription : 29/12/2009
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Sam 31 Mar 2018 - 12:37 Sam 31 Mar 2018 - 12:37 | |
| Impressionnant, Papydall !
Je suis justement en train de me battre avec les courves Bézier, dans le cadre de mon outil FlowChartDesigner. Je trace les liens entre les différents éléments d'un diagramme, soit à l'aide de segments perpendiculaires de droites, soit à l'aide de courbes Bézier. Dans les deux cas, il y a une flèche au bout pour indiquer la direction.
Mon problème est de trouver la bonne pente pour la flèche, en arrivant au point de destination. En considérant le dernier segment d'une courbe Bézier cubique, on a 4 points: départ en P0, deux points attracteurs P1 et P2 et finalement P3 comme point de destination. Ce qui est facile, c'est de prendre la pente du vecteur P2->P3, dessiner la flèche, puis reculer P3 jusqu'au centre de la base de la lfèche en un P3prime virtuel et dessiner la courbe Bézier P0(P1,p2)P3prime.
Sauf que l'inclinaison est totalement contre-intuituive - elle ne rend pas du tout compte de l'impression visuelle que donne l'arrivée de la courbe, sans dessiner la flèche.
Ce qu'il faudrait faire, ce serait de dessiner un cercle autour de P3 d'un rayon égal à la longueur de la flèche, déterminer le point d'intersection P3prime entre ce cercle et la courbe Bézier P0(P1,P2)P3, puis dessiner la flèche selon le vecteur P3prime->P3. Problème: comment déterminer P3prime dans ce modèle ? Je n'ai pas réussi, et sur un autre forum où j'ai posé la question, il n'y a pas de réponse non plus, pour le moment? Est-ce que tu aurais une idée ? | |
|   | | jjn4

Nombre de messages : 2747
Date d'inscription : 13/09/2009
 |  Sujet: +++ Sujet: +++  Sam 31 Mar 2018 - 15:16 Sam 31 Mar 2018 - 15:16 | |
| Toujours joli, le travail de Papydall !  | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Sam 31 Mar 2018 - 18:36 Sam 31 Mar 2018 - 18:36 | |
| Merci pour le compliment JJN4. @ Klaus. J’ai vu ta discussion avec les membres de Developpez.com sur ce siteJ’ai suivi la discussion avec intérêt : Il est toujours enrichissant de suivre des gens qui savent de quoi ils parlent. Il y a, entre autres, question de la tangente à la courbe de Bézier. Tu as posé la question : - Citation :
- A la limite, si je connaissais la pente de l'arrivée de la courbe, je pourrais faire quelque chose, mais tout cela est totalement caché.
Si ça peut t’aider ou simplement te donner une idée, voici comment déterminer l’équation de la tangente à la courbe de Bézier au point terminal. P0(x0,y0), P1(x1,y1), P2(x2,y2) et P3(x3,y3) sont les 4 points qui définissent la courbe de Bézier cubique. On peut calculer l’équation de la tangente à la courbe au point terminal P3(x3,y3). En effet la tangente passe par les 2 points P2(x2,y2) et P3(x3,y3) La droite passant par ces 2 points a pour équation : Y = f(x) = mx + p Déterminons la pente m : m = (y3 – y2) / (x3 – x2) Déterminons l’Ordonnée à l’origine p : p = y2 – mx2 D’où l’équation de la tangente à la courbe de Bézier passant par le point terminal est : Y = (y3 – y2) * x / (x3 –x2) + y2 – x2 * (y3 –y2) / (x3 –x2)
Dernière édition par papydall le Sam 31 Mar 2018 - 19:13, édité 1 fois | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Sam 31 Mar 2018 - 19:11 Sam 31 Mar 2018 - 19:11 | |
| Voici un exemple de tracé d'une courbe de Bézier et de sa tangente au point terminal. - Code:
-
rem ============================================================================
rem Tracé d’une courbe de Bézier et de sa tangente au point terminal
rem ============================================================================
dim x,y,x0,y0,x1,y1,x2,y2,x3,y3
picture 10 : full_space 10 : 2d_target_is 10 : print_target_is 10 : color 10,0,0,0
font_bold 10 : font_name 10,"arial" : font_color 10,0,255,0 : 2d_fill_off
' Exemple de courbe de Bézier cubique
x0 = 100 : y0 = 300
x1 = 120 : y1 = 100
x2 = 300 : y2 = 100
x3 = 400 : y3 = 300
2d_pen_color 255,000,000 : Cubic_Bezier_Curve(x0,y0,x1,y1,x2,y2,x3,y3)
2d_pen_color 255,255,000 : Equation_Tangente(x2,y2,x3,y3)
end
rem ============================================================================
' Equation de la courbe passant par 2 points (x1,y1) et (x2,y2)
SUB Equation_Tangente(x1,y1,x2,y2)
dim_local x,y,m,p
m = (y2 - y1) / (x2 - x1)
p = y1 - m * x1
' Voici l'équation de la tangente à la courbe de Bézier.
' Le point de tangence se trouve au point terminal.
rem _______________
rem | |
rem | y = m*x + p |
rem |_______________|
rem
' Tracé de la tangente
x = 0 : y = m*x+p : 2d_poly_from x,y
x = width(10) : y = m*x+p : 2d_poly_to x,y
END_SUB
rem ============================================================================
' Fonction retournant le cube de son argument
FNC Cube(n)
result n*n*n
END_FNC
rem ============================================================================
' Fonction retournant le carré de son argument
FNC Carre(n)
result n*n
END_FNC
rem ============================================================================
rem ============================================================================
' Tracé d'une courbe de Bézier cubique (de degré 3)
SUB Cubic_Bezier_Curve(x0,y0,x1,y1,x2,y2,x3,y3)
dim_local np
np = 100 : ' nombre de points interpolés sur la courbe,
' plus ce nombre est grand, plus la courbe sera lisse
dim_local bezier(np,2) : ' Tableau des coordonnées des points de la courbe
dim_local i,t,xp0,xp1,xp2,xp3,yp0,yp1,yp2,yp3
2d_poly_from x0,y0 : ' Point de départ du tracé
for i = 0 to np
t = i/np : ' t varie entre 0.0 et 1.0
xp0 = Cube(1-t)*x0 : yp0 = Cube(1-t)*y0
xp1 = 3*Carre(1-t)*t*x1 : yp1 = 3*Carre(1-t)*t*y1
xp2 = 3*(1-t)*Carre(t)*x2 : yp2 = 3*(1-t)*Carre(t)*y2
xp3 = Cube(t)*x3 : yp3 = Cube(t)*y3
bezier(i,0) = xp0 + xp1 + xp2 + xp3 : ' Coordonnées x(t)
bezier(i,1) = yp0 + yp1 + yp2 + yp3 : ' Coordonnées y(t)
2d_poly_to bezier(i,0),bezier(i,1) : ' Relier la courbe au point (x(t),y(t))
display
next i
2d_circle x0,y0,5 : 2d_circle x1,y1,5 : 2d_circle x2,y2,5 : 2d_circle x3,y3,5
print_locate x0-10,y0+10 : print "P0"
print_locate x1-10,y1+10 : print "P1"
print_locate x2+15,y2+10 : print "P2"
print_locate x3+15,y0+10 : print "P3"
END_SUB
rem ============================================================================
| |
|   | | Klaus

Nombre de messages : 12331
Age : 75
Localisation : Ile de France
Date d'inscription : 29/12/2009
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Sam 31 Mar 2018 - 19:35 Sam 31 Mar 2018 - 19:35 | |
| Merci de te plonger dans ce problème, Papydall.
Mais en réalité, la tangente, au point d'arrivée, correspond exactement à la pente du vecteur P2->P3. C'est ce que j'ai expliqué plusieurs fois, sur l'autre forum. Or, cela ne me satisfait pas. En effet, si tu traces, au point d'arrivée, une flèche de n pixels de haut, son axe central est tel que l'arrivée de la courbe sur le fond de la flèche est décalé, quelques fois même sérieusement. Fais l'essai avec une flèche de 10 pixels de haut et une largeur de 10 pixels à sa base. Puis, place P2 à la verticale de P3. Tu verras immédiatement que la pente de la flèche est verticale, alors que l'arrivée de la courbe donne une impression visuelle différente, et de fait, ette n'arrive pas au centre de la base de la flèche.
C'est pourquoi j"ai proposé la construction (imaginaire) avec un cercle d'un rayon de la hauteur de la flèche, autour du point P3. Et l'intersection de ce cercle avec la courbe donne un point P3prime. Le vecteur P3prime->p3 donne l'orientation et la longueur de la flèche. Il ne reste plus qu'à dessiner la courbe P0(P1,P2)P3prime pour avoir un résultat visuel impeccable. Et c'est là que j'ai le problème: déterminer mathématiquement ce point P3prime. | |
|   | | Klaus

Nombre de messages : 12331
Age : 75
Localisation : Ile de France
Date d'inscription : 29/12/2009
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Dim 1 Avr 2018 - 1:41 Dim 1 Avr 2018 - 1:41 | |
| Sur l'autre forum, un membre a eu l'idée géniale de calculer (sans les dessiner) les points de la courbe à l'envers, en partant de P3, de déterminer à chaque point la distance vers le point P3 et de s'arrêter dès que cette distance est égale ou supérieure à la longueur de la flèche. Ceci donne automatiquement mon si cher point P3prime, et j'ai pu dessiner une flèche indiquant visuellement la pente de l'arrivée subjective de la courbe, même dans le cas où P2 est à l'aplomb de P3. Pour moi, cette question esr réglé, et je vais iintégrer cela dans mon outil de dessin d'organigramme. En tout cas, merci d'avoir passé du temps sur ce problème, Papydall ! Pour le plaisir, voici le résultat: 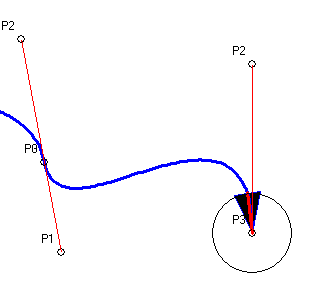 J'ai tracé une ligne rouge dans la flèche pour indiquer la pente de la flèche, manifestement différente de la pente du vecteur P2->P3. | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Dim 1 Avr 2018 - 2:46 Dim 1 Avr 2018 - 2:46 | |
| C’est génial comme solution ! Merci à tous ceux qui ont participé à enrichir la discussion et à apporter leurs idées . j’ai suivi avec intérêt la discussion sur l’autre forum. Merci à toi, Klaus pour ta persévérance et ton amour pour affronter les challenges. A un autre challenge qui ne tardera pas à se présenter !  | |
|   | | Oscaribout
Nombre de messages : 471
Date d'inscription : 29/12/2016
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Dim 1 Avr 2018 - 12:49 Dim 1 Avr 2018 - 12:49 | |
| Bonjour, Je ne suis vraiment pas à la hauteur pour répondre à ce poste. Mais en voyant le schéma dès le départ de la courbe de Papydall, je me suis demandé si garder une information à un moment du traçage de la courbe, cela pouvait être une solution. apparemment si j'ai bien compris, on trace la courbe en entier, et après on remonte pour trouver le point. Est-ce que cela est la même chose dans le résultat? - reprise du code de Papydall:
- Code:
-
rem ============================================================================
rem Tracé d’une courbe de Bézier et de sa tangente au point terminal
rem ============================================================================
dim x,y,x0,y0,x1,y1,x2,y2,x3,y3
picture 10 : full_space 10 : 2d_target_is 10 : print_target_is 10 : color 10,0,0,0
font_bold 10 : font_name 10,"arial" : font_color 10,0,255,0 : 2d_fill_off
' Exemple de courbe de Bézier cubique
x0 = 100 : y0 = 300
x1 = 120 : y1 = 100
x2 = 300 : y2 = 100
x3 = 400 : y3 = 300
2d_pen_color 255,000,000 : Cubic_Bezier_Curve(x0,y0,x1,y1,x2,y2,x3,y3)
2d_pen_color 255,255,000 : Equation_Tangente(x2,y2,x3,y3)
end
rem ============================================================================
' Equation de la courbe passant par 2 points (x1,y1) et (x2,y2)
SUB Equation_Tangente(x1,y1,x2,y2)
dim_local x,y,m,p
m = (y2 - y1) / (x2 - x1)
p = y1 - m * x1
' Voici l'équation de la tangente à la courbe de Bézier.
' Le point de tangence se trouve au point terminal.
rem _______________
rem | |
rem | y = m*x + p |
rem |_______________|
rem
' Tracé de la tangente
x = 0 : y = m*x+p : 2d_poly_from x,y
x = width(10) : y = m*x+p : 2d_poly_to x,y
END_SUB
rem ============================================================================
' Fonction retournant le cube de son argument
FNC Cube(n)
result n*n*n
END_FNC
rem ============================================================================
' Fonction retournant le carré de son argument
FNC Carre(n)
result n*n
END_FNC
rem ============================================================================
rem ============================================================================
' Tracé d'une courbe de Bézier cubique (de degré 3)
SUB Cubic_Bezier_Curve(x0,y0,x1,y1,x2,y2,x3,y3)
dim_local np
np = 100 : ' nombre de points interpolés sur la courbe,
' plus ce nombre est grand, plus la courbe sera lisse
dim_local bezier(np,2) : ' Tableau des coordonnées des points de la courbe
dim_local i,t,xp0,xp1,xp2,xp3,yp0,yp1,yp2,yp3
2d_poly_from x0,y0 : ' Point de départ du tracé
for i = 0 to np
t = i/np : ' t varie entre 0.0 et 1.0
xp0 = Cube(1-t)*x0 : yp0 = Cube(1-t)*y0
xp1 = 3*Carre(1-t)*t*x1 : yp1 = 3*Carre(1-t)*t*y1
xp2 = 3*(1-t)*Carre(t)*x2 : yp2 = 3*(1-t)*Carre(t)*y2
xp3 = Cube(t)*x3 : yp3 = Cube(t)*y3
bezier(i,0) = xp0 + xp1 + xp2 + xp3 : ' Coordonnées x(t)
bezier(i,1) = yp0 + yp1 + yp2 + yp3 : ' Coordonnées y(t)
2d_poly_to bezier(i,0),bezier(i,1) : ' Relier la courbe au point (x(t),y(t))
display
if i = 95
message "bezier(i,0) = " + str$(bezier(i,0)) + " bezier(i,1) = "+str$(bezier(i,1))
2d_circle bezier(i,0),bezier(i,1),10
end_if
next i
2d_circle x0,y0,5 : 2d_circle x1,y1,5 : 2d_circle x2,y2,5 : 2d_circle x3,y3,5
print_locate x0-10,y0+10 : print "P0"
print_locate x1-10,y1+10 : print "P1"
print_locate x2+15,y2+10 : print "P2"
print_locate x3+15,y0+10 : print "P3"
END_SUB
rem ============================================================================
C'est seulement pour savoir si j'ai bien compris. Quand au traçage du triangle, je ne suis plus dans la course. Il me faut du temps pour y arriver et c'est pas le sujet du moment.
Dernière édition par Oscaribout le Dim 1 Avr 2018 - 12:50, édité 1 fois (Raison : mauvaise orthographe dans le nom de Papydall) | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  Dim 1 Avr 2018 - 13:37 Dim 1 Avr 2018 - 13:37 | |
| Bonjour Oscaribout et merci pour ta contribution. - Citation :
- si j'ai bien compris, on trace la courbe en entier, et après on remonte pour trouver le point. Est-ce que cela est la même chose dans le résultat?
Tu as tout compris et ton idée est aussi bonne. Il fallait y penser ! J’ai modifié le code pour observer le tracé de la courbe et j’ai profité pour corriger un bug si la tangente est verticale (erreur de division par zéro) - Code:
-
rem ============================================================================
rem Tracé d’une courbe de Bézier et de sa tangente au point terminal
rem ============================================================================
dim x,y,x0,y0,x1,y1,x2,y2,x3,y3
picture 10 : full_space 10 : 2d_target_is 10 : print_target_is 10 : color 10,0,0,0
font_bold 10 : font_name 10,"arial" : font_color 10,0,255,0 : 2d_fill_off
' Exemple de courbe de Bézier cubique
x0 = 100 : y0 = 300
x1 = 320 : y1 = 020
x2 = 550 : y2 = 100
x3 = 400 : y3 = 300
2d_pen_color 255,000,000 : Cubic_Bezier_Curve(x0,y0,x1,y1,x2,y2,x3,y3)
2d_pen_color 255,255,000 : Equation_Tangente(x2,y2,x3,y3)
end
rem ============================================================================
' Equation de la courbe passant par 2 points (x1,y1) et (x2,y2)
SUB Equation_Tangente(x1,y1,x2,y2)
dim_local x,y,m,p,epsilon
epsilon = power(10,0-10)
if x2 = x1 then x2 = x2 + epsilon : ' pour éviter la division par 0 quand la tangente est verticale
m = (y2 - y1) / (x2 - x1)
p = y1 - m * x1
' Voici l'équation de la tangente à la courbe de Bézier.
' Le point de tangence se trouve au point terminal.
rem _______________
rem | |
rem | y = m*x + p |
rem |_______________|
rem
' Tracé de la tangente
x = 0 : y = m*x+p : 2d_poly_from x,y
x = width(10) : y = m*x+p : 2d_poly_to x,y
END_SUB
rem ============================================================================
' Fonction retournant le cube de son argument
FNC Cube(n)
result n*n*n
END_FNC
rem ============================================================================
' Fonction retournant le carré de son argument
FNC Carre(n)
result n*n
END_FNC
rem ============================================================================
' Tracé d'une courbe de Bézier cubique (de degré 3)
SUB Cubic_Bezier_Curve(x0,y0,x1,y1,x2,y2,x3,y3)
dim_local np
np = 100 : ' nombre de points interpolés sur la courbe,
' plus ce nombre est grand, plus la courbe sera lisse
dim_local bezier(np,2) : ' Tableau des coordonnées des points de la courbe
dim_local i,t,xp0,xp1,xp2,xp3,yp0,yp1,yp2,yp3
2d_poly_from x0,y0 : ' Point de départ du tracé
for i = 0 to np
t = i/np : ' t varie entre 0.0 et 1.0
xp0 = Cube(1-t)*x0 : yp0 = Cube(1-t)*y0
xp1 = 3*Carre(1-t)*t*x1 : yp1 = 3*Carre(1-t)*t*y1
xp2 = 3*(1-t)*Carre(t)*x2 : yp2 = 3*(1-t)*Carre(t)*y2
xp3 = Cube(t)*x3 : yp3 = Cube(t)*y3
bezier(i,0) = xp0 + xp1 + xp2 + xp3 : ' Coordonnées x(t)
bezier(i,1) = yp0 + yp1 + yp2 + yp3 : ' Coordonnées y(t)
2d_poly_to bezier(i,0),bezier(i,1) : ' Relier la courbe au point (x(t),y(t))
pause 100
if i = np-5
message "bezier(i,0) = " + str$(bezier(i,0)) + " bezier(i,1) = "+str$(bezier(i,1))
2d_circle bezier(i,0),bezier(i,1),10
end_if
next i
2d_circle x0,y0,5 : 2d_circle x1,y1,5 : 2d_circle x2,y2,5 : 2d_circle x3,y3,5
print_locate x0-10,y0+10 : print "P0"
print_locate x1-10,y1+10 : print "P1"
print_locate x2+15,y2+10 : print "P2"
print_locate x3+15,y0+10 : print "P3"
END_SUB
rem ============================================================================
| |
|   | | Contenu sponsorisé
 |  Sujet: Re: Les Courbes de Bézier cubiques Sujet: Re: Les Courbes de Bézier cubiques  | |
| |
|   | | | | Les Courbes de Bézier cubiques |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
