| Novembre 2024 | | Lun | Mar | Mer | Jeu | Ven | Sam | Dim |
|---|
| | | | | 1 | 2 | 3 | | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | 11 | 12 | 13 | 14 | 15 | 16 | 17 | | 18 | 19 | 20 | 21 | 22 | 23 | 24 | | 25 | 26 | 27 | 28 | 29 | 30 | |  Calendrier Calendrier |
|
|
| | Demande d'aide en maths. |  |
| | | Auteur | Message |
|---|
Pedro

Nombre de messages : 1595
Date d'inscription : 19/01/2014
 |  Sujet: Demande d'aide en maths. Sujet: Demande d'aide en maths.  Mer 14 Déc 2016 - 17:04 Mer 14 Déc 2016 - 17:04 | |
| Bonjour.
Il m'est demandé de résoudre le problème suivant:
Soit un mur situé à gauche, d'une hauteur d'un mètre et un mur à droite, d'une hauteur de 1,5 mètre.
Une échelle est posée contre le mur de droite, sa base se situe dans le coin en bas à gauche (base du mur de gauche).
Une autre échelle est posée contre le mur de gauche, sa base se situe dans le coin en bas à droite (base du mur de droite).
Le sommets des 2 échelles se situant à l'extrémité haute des murs.
On connaît ce qui suit:
Hauteur du mur de gauche: 1m
Hauteur du mur de droit: 1,5m
Il est demandé à quelle hauteur les 2 échelles se croisent.
Merci de votre aide. | |
|   | | Jean Claude

Nombre de messages : 5950
Age : 70
Localisation : 83 Var
Date d'inscription : 07/05/2009
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Mer 14 Déc 2016 - 17:20 Mer 14 Déc 2016 - 17:20 | |
| Si les 2 murs sont parallèles, les échelles se croisent à la diagonale du carré dont le coté est égal à la hauteur du mur le plus petit.
|/|
A+ | |
|   | | Yannick
Nombre de messages : 8635
Age : 53
Localisation : Bretagne
Date d'inscription : 15/02/2010
 |  Sujet: re Sujet: re  Mer 14 Déc 2016 - 18:07 Mer 14 Déc 2016 - 18:07 | |
| heu...il manque pas la distance entre les deux murs ?.... Edit: j' ai dit une c....rie...désolé  | |
|   | | Jean Claude

Nombre de messages : 5950
Age : 70
Localisation : 83 Var
Date d'inscription : 07/05/2009
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Mer 14 Déc 2016 - 18:12 Mer 14 Déc 2016 - 18:12 | |
| Ben oui, mais alors il faudrait aussi la hauteur des échelles car dans l'énoncé du problème il est dit: Le sommets des 2 échelles se situant à l'extrémité haute des murs. Il n'en reste pas moins, qui si les échelles sont de même hauteur, c'est bien le croisement des 2 diagonales (du "petit" carré) qui est demandé.
suivant la hauteur des échelles, on peut se retrouvé avec un rectangle. En fait c'est simple: la réponse est 50 cm car le coté du rectangle (ou du carré) est égale à la hauteur du petit mur. Les échelles vont donc se croiser à la moitié de la hauteur du petit mur de 1m, à condition que les 2 échelles soit de même longueur. Heu.. ben.. je crois.    | |
|   | | Jean Claude

Nombre de messages : 5950
Age : 70
Localisation : 83 Var
Date d'inscription : 07/05/2009
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Mer 14 Déc 2016 - 18:29 Mer 14 Déc 2016 - 18:29 | |
| | |
|   | | Pedro

Nombre de messages : 1595
Date d'inscription : 19/01/2014
 |  Sujet: Demande d'aide en maths. Sujet: Demande d'aide en maths.  Mer 14 Déc 2016 - 19:43 Mer 14 Déc 2016 - 19:43 | |
| Bonsoir.
Je rappelle que, dans ce devoir, la hauteur des échelles n'est pas connue ! | |
|   | | Marc

Nombre de messages : 2466
Age : 63
Localisation : TOURS (37)
Date d'inscription : 17/03/2014
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Mer 14 Déc 2016 - 21:31 Mer 14 Déc 2016 - 21:31 | |
| Bonsoir à tous, Au risque de dire une bêtise, je pense que les échelles se croiseront toujours à la même hauteur quelle que soit la distance entre les murs, soit à 60cm du sol. Je continue de réfléchir... Edit : Au final, confirmé par mes enfants et avec la complicité de Thalès, nous avons : a = Mur gauche = 150 cm b = Mur droit = 100 cm h = Hauteur du point de croisement
. b x a 100 x 150 1500
h = --------- = ------------- = --------- = 60 cm
. b + a 100 + 150 250En espérant que le maçon a utilisé un fil à plomb 
Dernière édition par Marc37 le Jeu 15 Déc 2016 - 13:40, édité 2 fois | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Jeu 15 Déc 2016 - 0:40 Jeu 15 Déc 2016 - 0:40 | |
| Salut tout le monde. @Pedro Alvarez Le code suivant schématise le problème. Est-ce bien ça ? Si oui, la solution est indéterminée car il manque une autre donnée : soit la largeur du couloir AD (voir le résultat du code), soit la longueur de l’une de deux échelles. - Code:
-
width 0,700
2d_line 100,400,400,400
2d_line 150,400,150,200
2d_line 350,400,350,100
2d_line 150,400,350,100
2d_line 350,400,150,200
2d_line 230,282,230,400
print_locate 140,410 : print "A"
print_locate 140,190 : print "B"
print_locate 360,090 : print "C"
print_locate 350,410 : print "D"
print_locate 220,272 : print "I"
print_locate 220,410 : print "H"
print_locate 450,100 : print "Données : "
print_locate 450,120 : print "AB = 1 m : hauteur du mur à gauche"
print_locate 450,140 : print "DC = 1.5 m : hauteur du mur = droite"
print_locate 450,160 : print "AC = ? : longueur de la 1ère l'échelle"
print_locate 450,180 : print "DB = ? : longueur de la seconde échelle"
print_locate 450,200 : print "I : point de croisement de deux échelles"
print_locate 450,220 : print "H : projection orthogonale de I sur le sol"
print_locate 450,250 : print "On demande la hauteur IH"
end
| |
|   | | Marc

Nombre de messages : 2466
Age : 63
Localisation : TOURS (37)
Date d'inscription : 17/03/2014
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Jeu 15 Déc 2016 - 0:49 Jeu 15 Déc 2016 - 0:49 | |
| Bonsoir Papydall, nos messages se sont croisés : j'étais en train d"éditer mon dernier message.
| |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Jeu 15 Déc 2016 - 1:07 Jeu 15 Déc 2016 - 1:07 | |
| Salut Marc - Citation :
- Au risque de dire une bêtise, je pense que les échelles se croiseront toujours à la même hauteur quelque soit la distance entre les murs, soit à 60cm du sol.
Je ne pense pas! La hauteur à laquelle les échelles (qui sont non dilatables) se croisent dépend nécessairement de la distance entre les murs. | |
|   | | Yannick
Nombre de messages : 8635
Age : 53
Localisation : Bretagne
Date d'inscription : 15/02/2010
 |  Sujet: re Sujet: re  Jeu 15 Déc 2016 - 1:40 Jeu 15 Déc 2016 - 1:40 | |
| finalement, je n' avais pas dit de bêtise...  | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Jeu 15 Déc 2016 - 3:00 Jeu 15 Déc 2016 - 3:00 | |
| Non ygeronimi, tu n'as pas dit de bêtise.
Je connaissais cette énigme sous le nom : « énigme à deux échelles » parue dans Science et Vie dans les années 80 du siècle dernier.
On donnait les longueurs de deux échelles (3 et 2 m) qui se croisent à 1 m et on demandait la largeur du couloir.
La solution aboutit à une équation du 4ème degré résoluble par la méthode de Ferrari.
Je crois que j'ai posté (où ? Quand ? Je ne me rappelle plus) un programme de résolution de l'équation du 4ème dégré. | |
|   | | Jean Claude

Nombre de messages : 5950
Age : 70
Localisation : 83 Var
Date d'inscription : 07/05/2009
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Jeu 15 Déc 2016 - 9:43 Jeu 15 Déc 2016 - 9:43 | |
| Salut à tous, Je n'ai pas non plus de solution universelle, mais sous certaines conditions j'ai trouvé une approche. - Code:
-
width 0,650 : height 0,580
' font_bold 0
dim AB% : AB%=100:' mur de 1m
dim CD% : CD%=150:' mur de 1.50m
dim x1%,y1% : x1%=260 : y1%=260:' point A
dim x2%,y2% : x2%=260+AB% : y2%=260:' point C
dim r1%,r2% : r1%=AB% : r2%=CD%
2d_fill_off
2d_circle x1%,y1%,5 : 2d_circle x1%,y1%,r1% : print_locate x1%,y1%+10 : print "A"
2d_circle x2%,y2%,5 : 2d_circle x2%,y2%,r2% : print_locate x2%,y2%+10 : print "C"
print_locate 10,10 : print "MUR 1: AB=100 Px"
print_locate 10,30 : print "MUR 2: CD=150 Px"
2d_pen_dash
2d_line x1%-200,y1%,x2%+200,y2%
2d_pen_solid
2d_pen_width 2
2d_line x1%,y1%,x2%,y2%: ' Espace entre les murs =AB%
print_locate 10,50 : print "Espace entre les murs = AB donc 100 Px"
' Les murs
2d_pen_width 4
2d_line x1%,y1%,x2%-AB%,y2%-AB% : print_locate (x2%-AB%)-10,y2%-AB% : print "B"
2d_line x2%,y2%,x2%,y2%-CD% : print_locate x2%-5,y2%-(CD%+15) : print "D"
' les échelles
2d_pen_width 2
2d_line x1%,y1%,x2%,y2%-CD%
2d_line x2%,y2%,x1%,y1%-AB%
' cercle 3
2d_pen_width 1
dim x3%,y3% : x3%=260-AB% : y3%=260
2d_circle x3%,y3%,5 : 2d_circle x3%,y3%,(r2%+PI) : print_locate x3%-150,y3%+10 : print "Cercle 3: Centre=A-AB Rayon=CD+PI"
print_locate 10,480 : print "CONDITIONS: murs d'aplomd, échelles modulables en longueur ET SURTOUT => CD=AB+(AB/2)"
print_locate 10,500 : print "Mais je n'ai pas trouvé la formule, ce n'est qu'un dessin."
 A+ | |
|   | | Marc

Nombre de messages : 2466
Age : 63
Localisation : TOURS (37)
Date d'inscription : 17/03/2014
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Jeu 15 Déc 2016 - 10:49 Jeu 15 Déc 2016 - 10:49 | |
| Bonjour à tous !
Je vous ferai une photo de la feuille qui explique le développement mathématique qui donne au final :
. b x a 100 x 150 1500
h = --------- = ------------- = --------- = 60 cm
. b + a 100 + 150 250
Nous avons utilisé 2 fois Thalès pour résoudre cette énigme.
Pour l'instant je suis au boulot, je ne peux pas vous l'envoyer, il faut que je rentre à la maison.
Bonne journée et à ce soir sur le forum !
Sans transition :
Je remarque qu'ici, au boulot, je suis sous XP et je n'ai pas les émoticônes du forum, tout comme l'avait signalé notre ami Cosmos70.
Peut être est-il aussi sous XP ? | |
|   | | Marc

Nombre de messages : 2466
Age : 63
Localisation : TOURS (37)
Date d'inscription : 17/03/2014
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Jeu 15 Déc 2016 - 13:26 Jeu 15 Déc 2016 - 13:26 | |
| Voilà notre feuille de calcul familiale : 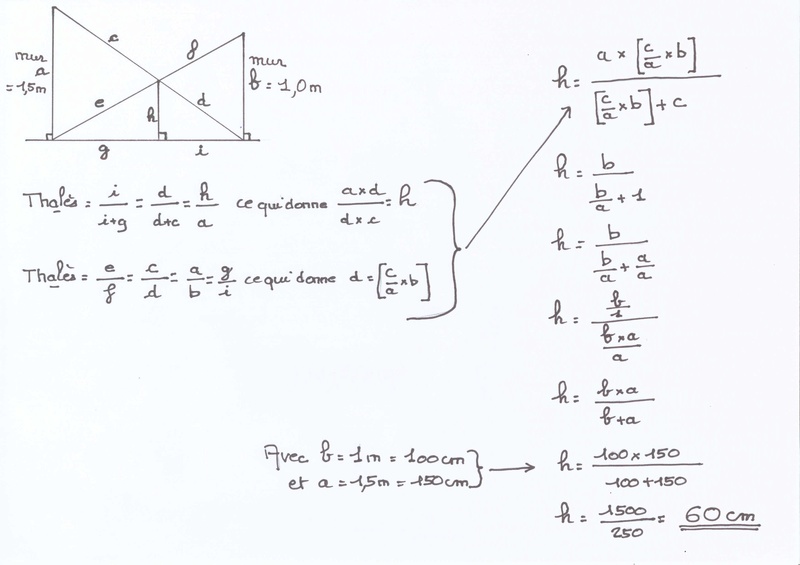 Peu importe la distance entre les 2 murs, la hauteur de croisement des échelles sera toujours la même (à 60 cm du sol dans notre cas). Reste à savoir si toute notre théorie est bonne ou fausse... Peut-être aurons-nous un zéro pointé ! Une précision, comme dit plus haut, il faut un bon maçon pour les murs : ils doivent être perpendiculaires au sol. A vos critiques... Je repars travailler. EDIT:Petite erreur de recopie à la fin de la première formulation de Thales un + un peu trop incliné est devenu un x. Il faut donc lire : a x d ------- = h d + c
Dernière édition par Marc37 le Jeu 15 Déc 2016 - 15:25, édité 2 fois | |
|   | | silverman

Nombre de messages : 970
Age : 52
Localisation : Picardie
Date d'inscription : 18/03/2015
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Jeu 15 Déc 2016 - 15:18 Jeu 15 Déc 2016 - 15:18 | |
| Bravo marc37, belle démonstration du théorème de thales! | |
|   | | Jean Claude

Nombre de messages : 5950
Age : 70
Localisation : 83 Var
Date d'inscription : 07/05/2009
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Jeu 15 Déc 2016 - 16:45 Jeu 15 Déc 2016 - 16:45 | |
| C'est beau les Maths, au début on a rien en poche et à la fin la solution. Connaitre le théorème de Thalès, c'est déjà trop pour moi, mais en plus, savoir que c'est lui qu'il fallait employer, alors là...    A+  | |
|   | | Yannick
Nombre de messages : 8635
Age : 53
Localisation : Bretagne
Date d'inscription : 15/02/2010
 |  Sujet: re Sujet: re  Jeu 15 Déc 2016 - 18:52 Jeu 15 Déc 2016 - 18:52 | |
| Bon, alors, finalement, j' ai dit une bêtise...  | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  Sam 17 Déc 2016 - 0:11 Sam 17 Déc 2016 - 0:11 | |
| Salut tout le monde. On peut également tenter de résoudre ce problème analytiquement. Si on rapporte le plan à un système d’axes orthonormé XOY, avec OX l’axe horizontal (le sol) et OY l’axe vertical représenté par le mur gauche, on peut facilement déterminer les deux équations de deux droites représentant les échelles, soit y1 et y2. En résolvant y1 = y2, on trouvera x qui est la coordonnée horizontale (abscisse du point de croisement), puis en reportant cette valeur dans l’une ou l’autre des équations (y1 ou y2) on détermine la coordonnée verticale (ordonnée) du point de croisement qui n’est autre que la hauteur demandée. Soit d la distance entre les deux murs. Soit y1 l’équation de la droite représentant l’échelle adossée sur le mur droit. Cette droite passe par l’origine, donc elle est de la forme Y1 = a*x. Y1 passe par le point (d,1.5) a*d = 1.5 d’où a = 1.5/d Y1 = (1.5/d)*x Soit y2 l’équation de la droite représentant l’échelle adossée sur le mur gauche. Cette droite passe par les deux points (0,1) et (d,0) Son équation réduite est : y2 = a*x + b. La valeur de a (coefficient directeur) est donnée par : a = (0 -1) / d – 0) = -1/d Pour déterminer b (l’ordonnée à l’origine), il suffit de résoudre l’équation d’inconnue b : b = 1-(-1/d) *0 = 1, d’où y2 = (-1/d)*x + 1 Pour déterminer les coordonnées du point d’intersection de y1 et de y2, il faut que ce point vérifie en même temps l’équation de la première et celle de la seconde équation. On doit donc résoudre le système : Y = (1.5/d)*x (1) Y = (-1/d)*x + 1 (2) Avec d comme paramètre (rappel d désigne la largeur du couloir, c-à-d l’écart entre les 2 murs). Résolvons ce système par substitution en éliminant x dans les deux équations Multiplions l’équation (2) par 1.5 et ajoutons l’équation (1) à l’équation (2), ça donne : Y = (1.5/d)*x + 1.5* Y = (-1.5/d)*x +1.5 ------------------------------ 2.5*y = 1.5 D’où y = 1.5/2.5 = 3/5 Reportons cette valeur dans (1) ou dans (2), on obtient : (1) Donne : 3/5 = (1.5/d)*x === > x = (3/5)/(1.5/d) = 2*d/5 X = 2*d/5 et (2) donne également : 3/5 = (-1/d)*x+1 === > x = ( -2/5) / (-1/d) = 2*d/5 Le point d’intersection de deux droites (les échelles) est le point de coordonnées (2*d/5, 3/5) 2*d/5 correspond à l’abscisse (qui est fonction de d, la distance entre les murs). 3/5 correspond à l’ordonnée (qui est la hauteur recherchée) : c’est un nombre indépendant de d, la distance entres les murs. Remarque : Dans les calculs ci=dessus, j’ai utilisé le mètre comme unité de longueur. La hauteur calculée y = 3/5 = 0.6 unité de longueur, soit 60 cm. Cela confirme le résultat trouvé par les Marc37, père et fils que je salue profondément.  Voilà, Pedro Alvarez, ton problème est résolu. A un autre problème peut-être ? | |
|   | | Pedro

Nombre de messages : 1595
Date d'inscription : 19/01/2014
 |  Sujet: Demande d'aide en maths. Sujet: Demande d'aide en maths.  Sam 17 Déc 2016 - 7:39 Sam 17 Déc 2016 - 7:39 | |
| Bonjour à tous les panoramiciens.
Un grand merci à tous, le problème étant résolu.
Il s'agissait en fait d'un problème soumis à un élève de 3è, mais j'avoue ne pas avoir pû le résoudre seul. | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Demande d'aide en maths. Sujet: Re: Demande d'aide en maths.  | |
| |
|   | | | | Demande d'aide en maths. |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
