| Novembre 2024 | | Lun | Mar | Mer | Jeu | Ven | Sam | Dim |
|---|
| | | | | 1 | 2 | 3 | | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | 11 | 12 | 13 | 14 | 15 | 16 | 17 | | 18 | 19 | 20 | 21 | 22 | 23 | 24 | | 25 | 26 | 27 | 28 | 29 | 30 | |  Calendrier Calendrier |
|
|
| | Résolution des équations polynomiales de degré 1, 2, 3 et 4 |  |
| | | Auteur | Message |
|---|
papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Ven 13 Mar 2020 - 2:59 Ven 13 Mar 2020 - 2:59 | |
| Calculez ! Calculez! Il en restera toujours ! La suite est dans le code. - Code:
-
rem ============================================================================
rem Résolution des équations polynomiales de degré 1, 2, 3 et 4
rem Auteur : Papydall
rem Date de création : 12 / 03 / 2020
rem Dernière modification : 13 / 03 / 2020
rem ============================================================================
rem On s’interesse ici aux équations de degré inférieur à 5 qui sont résolubles
rem en utilisant les opérations habituelles +, -, *, / et racine nième.
rem La théorie d’Evariste Galois montre que les équations ne sont pas solubles
rem par radicaux à partir du cinquième degré
rem ============================================================================
rem D’après le théorème fondamental de l’algèbre des polynômes :
rem Tout polynôme de degré N admet exactement N solutions (on dit aussi racines
rem ou zéros).
rem Ces racines sont réelles ou complexes, simples ou multiples et si elles sont
rem complexes, elles sont conjuguées deux-à-deux.
rem Ce programme permet de résoudre un polynôme de degré <= à 4
rem ============================================================================
rem RAPPEL : un nombre complexe s’écrit sous la forme z = x + i*y , avec x et y
rem réels et i nombre imaginaire dont le carré vaut -1 (i² = -1).
rem x s’appelle partie réelle du nombre complexe z
rem y s’appelle partie imaginaire du nombre complexe z.
rem Si y = 0 , le nombre est réel.
rem Si x = 0 , le nombre est imaginaire pur.
rem Deux nombres complexes conjugués sont deux nombres complexes dont leurs
rem parties imaginaires sont de signes contraires.
rem ============================================================================
label choix,calculer,NbChiffres,Quitter
dim a,b,c,d,e,i,j,x1,x2,u,w,z,t,r,s,degre,nb,nbc,t$,plus$
dim complexe%,re,im,epsilon,delta,passe,aa,bb,cc,c2,d2,decal,p1,p2
epsilon = power(10,0-16)
nb = 3 : nbc = power(10,nb) : ' nombre de chiffres (par défaut) après la virgule
width 0,600 : height 0,500 : font_name 0,"arial black" : font_size 0,11
t$ = "Résolution des équations de degré < 5"
caption 0,t$ : application_title t$
alpha 5 : top 5,10 : left 5,80 : font_name 5,"dejavu sans mono" : font_color 5,0,0,255
caption 5,t$ : font_bold 5 : font_size 5,12
container_option 10 : top 10,50 : left 10,20 : caption 10,"Degré de l'équation"
font_name 10,"arial black" : font_color 10,255,255,0 : font_size 10,10 : color 10,150,100,20
option 11 : parent 11,10 : top 11,20 : left 11,10 : caption 11,"1er degré"
option 12 : parent 12,10 : top 12,40 : left 12,10 : caption 12,"2ème degré"
option 13 : parent 13,10 : top 13,60 : left 13,10 : caption 13,"3ème degré"
option 14 : parent 14,10 : top 14,80 : left 14,10 : caption 14,"4ème degré"
for i = 11 to 14 : font_color i,0,255,255 : on_click i,choix : next i
container 20 : top 20,50 : left 20,320 : caption 20,"Coefficients de l'équation"
width 20,250 : height 20,150 : font_name 20,"arial black" : font_size 20,10 : inactive 20
color 20, 150,100,20 : font_color 20,255,255,0
alpha 21 : parent 21,20 : top 21,030 : left 21,10 : caption 21,"a = "
edit 22 : parent 22,20 : top 22,030 : left 22,50
alpha 23 : parent 23,20 : top 23,050 : left 23,10 : caption 23,"b = "
edit 24 : parent 24,20 : top 24,050 : left 24,50
alpha 25 : parent 25,20 : top 25,070 : left 25,10 : caption 25,"c = "
edit 26 : parent 26,20 : top 26,070 : left 26,50
alpha 27 : parent 27,20 : top 27,090 : left 27,10 : caption 27,"d = "
edit 28 : parent 28,20 : top 28,090 : left 28,50
alpha 29 : parent 29,20 : top 29,110 : left 29,10 : caption 29,"e = "
edit 30 : parent 30,20 : top 30,110 : left 30,50
for i = 21 to 30 : hide i : next i
for i = 22 to 30 step 2 : font_color i,255,0,0 : next i
memo 40 : top 40, 220 : left 40,20 : width 40,550 : height 40,150
color 40,50,100,150 : font_name 40,"dejavu sans mono" : font_bold 40 : font_color 40,255,255,50
spin 50 : top 50,180 : left 50,240 : width 50,70 : min 50,3 : max 50,16 : position 50,3
on_change 50,NbChiffres
alpha 60 : top 60,180 : left 60,10 : caption 60,"Nb chiffres après la virgule "
button 98 : top 98,400 : left 98,050 : caption 98,"Calculer" : font_name 98,"arial black"
button 99 : top 99,400 : left 99,400 : caption 99,"Quitter" : font_name 99,"Arial black"
on_click 98,Calculer : inactive 98
on_click 99,Quitter
end
rem ============================================================================
NbChiffres:
nb = position(50)
nbc = power(10,nb)
gosub Calculer
return
rem ============================================================================
Choix:
for i = 21 to 30 : hide i : next i
select number_click
case 11 : j = 20+2*2 : for i = 21 to j : show i : next i : Degre = 1
for i = 22 to 24 step 2 : text i,"" : next i
case 12 : j = 20+3*2 : for i = 21 to j : show i : next i : Degre = 2
for i = 22 to 26 step 2 : text i,"" : next i
case 13 : j = 20+4*2 : for i = 21 to j : show i : next i : Degre = 3
for i = 22 to 28 step 2 : text i,"" : next i
case 14 : j = 20+5*2 : for i = 21 to j : show i : next i : Degre = 4
for i = 22 to 30 step 2 : text i,"" : next i
end_select
active 20 : active 98 : clear 40
set_focus 22
return
rem ============================================================================
Calculer:
clear 40
select degre
case 1 : Degre_1()
case 2 : Degre_2()
case 3 : Degre_3()
case 4 : Degre_4()
end_select
return
rem ============================================================================
SUB Degre_1()
if text$(22) = "" or text$(24) = ""
message "!!! Veuillez indiquer tous les coefficients !!!"
exit_sub
end_if
if numeric(text$(22)) = 0 or numeric(text$(24)) = 0
message "!!! Veuillez indiquer des valeurs numériques pour les coefficients !!!"
exit_sub
end_if
a = val(text$(22))
if a = 0
message "!!! La valeur de a doit être différente de zéro !!!" : exit_sub
end_if
b = val(text$(24)) : if b < 0 then plus$ = " " : else : plus$ = " + "
x1 = 0-b/a
if a = -1
t$ = "-x"
else
if a = 1
t$ = "x"
else
t$ = str$(a) + "x"
end_if
end_if
t$ = t$ + plus$ + str$(b) + " = 0 "
item_add 40,"L'équation du 1er degré : "
item_add 40, t$
item_add 40, "admet comme solution"
' formatage de la solution
x1 = x1 + sgn(x1)*epsilon : x1 = int(x1*nbc+0.5)/nbc
item_add 40,"x = " + str$(x1)
END_SUB
rem ============================================================================
SUB Degre_2()
dim_local a$,b$,c$
if text$(22) = "" or text$(24) = "" or text$(26) = ""
message "!!! Veuillez indiquer tous les coefficients !!!"
exit_sub
end_if
if numeric(text$(22)) = 0 or numeric(text$(24)) = 0 or numeric(text$(24)) = 0
message "!!! Veuillez indiquer des valeurs numériques pour les coefficients !!!"
exit_sub
end_if
a = val(text$(22))
if a = 0
message "!!! La valeur de a doit être différente de zéro !!!"
exit_sub
end_if
b = val(text$(24))
c = val(text$(26))
if a = 1 then a$ = "x² " : else : a$ = str$(a)+"x² " : ' Pour ne pas afficher 1x²
if a = -1 then a$ = "-x²" : ' pour ne pas afficher -1x²
if b = 1 then b$ = "+ x " : else : b$ = str$(b)+"x " : ' Pour ne pas afficher 1x
if b = -1 then b$ = "- x " : ' pour ne pas afficher -1x
if b > 1 then b$ = "+" + str$(b) + "x "
if b = 0 then b$ = ""
if c = 0 then c$ = " = 0" : else : c$ = str$(c) + " = 0 :"
if c > 0 then c$ = "+" + c$
item_add 40,"L'équation du deuxième degré"
item_add 40, a$+b$+c$
item_add 40, "admet comme solutions :"
Equat2(a,b,c)
' formatage des solutions
x1 = x1 + sgn(x1)*epsilon : x1 = int(x1*nbc+0.5)/nbc
x2 = x2 + sgn(x2)*epsilon : x2 = int(x2*nbc+0.5)/nbc
re = re + sgn(re)*epsilon : re = int(re*nbc+0.5)/nbc
im = im + sgn(im)*epsilon : im = int(im*nbc+0.5)/nbc
if complexe% = 0 : ' Les racines sont-elles réelles ?
' oui, les racines sont réelles
if x1 = x2 : ' est-ce une racine double ?
item_add 40, "Une racine réelle double :"
item_add 40, "X1 = X2 = " + str$(x1)
else : ' les racines sont distinctes
item_add 40, "Deux racines réelles distinctes :"
item_add 40,"X1 = " + str$(x1)
item_add 40,"X2 = " + str$(x2)
end_if
else : ' les racines sont belles et bien complexes
item_add 40,"Deux racines complexes conjuguées :"
item_add 40,"X1 = " + str$(re) + " + " + str$(im) + "i"
item_add 40,"X2 = " + str$(re) + " - " + str$(im) + "i"
end_if
END_SUB
rem ============================================================================
' Résolution de l'équation du second degré : ax² + bx + c = 0
SUB Equat2(a,b,c)
dim_local p,q,delta : ' variables locales utilisées pour le calcul
p = b/a : q = c/a : delta = (p/2)*(p/2)-q
if delta < 0 : ' les racines sont complexes conjuguées
complexe% = 1 : ' on met le flag à 1
delta = abs(delta) : ' On prend la valeur absolue pour le calcul
re = 0-(p/2) : im = sqr(delta) : ' parties réelle et imaginaire de la solution
else : ' les racines sont réelles
complexe% = 0
x1 = 0-(p/2) + sqr(delta) : x2 = 0-(p/2) - sqr(delta) : ' calcul des 2 racines
end_if
END_SUB
rem ============================================================================
SUB Degre_3()
dim_local a$,b$,c$,d$
if text$(22) = "" or text$(24) = "" or text$(26) = "" or text$(26) = ""
message "!!! Veuillez indiquer tous les coefficients !!!"
exit_sub
end_if
if numeric(text$(22)) = 0 or numeric(text$(24)) = 0 or numeric(text$(24)) = 0 or numeric(text$(26)) = 0
message "!!! Veuillez indiquer des valeurs numériques pour les coefficients !!!"
exit_sub
end_if
a = val(text$(22))
if a = 0
message "!!! La valeur de a doit être différente de zéro !!!"
exit_sub
end_if
b = val(text$(24)) : c = val(text$(26)) : d = val(text$(28))
if a = 1 then a$ = "x³ " : else : a$ = str$(a) + "x³" : ' Pour ne pas afficher 1x³
if a = -1 then a$ = "-x³ " : ' pour ne pas afficher -1x³
if b = 1 then b$ = "+x² " : else : b$ = str$(b) + "x²" : ' Pour ne pas afficher 1x²
if b = -1 then b$ = "-x² " : ' pour ne pas afficher -1x²
if b > 1 then b$ = "+ " + str$(b) + "x² "
if b = 0 then b$ = ""
if c = 1 then c$ = "+x " : else : c$ = str$(c) + "x" : ' pour ne pas afficher 1x
if c = -1 then c$ = "-x " : ' pour ne pas afficher -1x
if c > 1 then c$ = "+" + str$(c) + "x "
if c = 0 then c$ = ""
if d = 0 then d$ = " = 0" : else : d$ = str$(d)+" = 0"
if d > 0 then d$ = "+" + d$
item_add 40,"L'équation du troisième degré"
item_add 40, a$+b$+c$+d$
item_add 40, "admet comme solutions :"
Equat3(a,b,c,d)
END_SUB
rem ============================================================================
SUB Equat3(a,b,c,d)
dim_local a0,a1,a2,a3,p,q
dim_local delta,w,w1,x1,x2,x3
dim_local u,v,t,i$
' cas trivial
if b = 0 and c = 0 and d = 0
item_add 40,"Une racine triple"
item_add 40,"x1 = x2 = x3 = 0"
exit_sub
end_if
if b = 0 and c = 0 : ' l'algorithme général ne fonctionne pas pour ce cas particulier.
' Les 3 solutions particulières sont :
' une racine réelle
x1 = sgn(0-d/a)*power(abs(d/a),1/3) : ' racine cubique de -d/a
' et 2 racines complexes conjuguées
re = 0-x1/2 : im = x1*sqr(3)/2
' formatage des solutions
x1 = x1 + sgn(x1)*epsilon : x1 = int(x1*nbc+0.5)/nbc
re = re + sgn(re)*epsilon : re = int(re*nbc+0.5)/nbc
im = im + sgn(im)*epsilon : im = int(im*nbc+0.5)/nbc
' affichage des solutions
item_add 40,"une racine réelle et deux racines complexes conjuguées"
item_add 40,"x1 = " + str$(x1)
item_add 40,"x2 = " + str$(re) + " + i * " + str$(im)
item_add 40,"x3 = " + str$(re) + " - i * " + str$(im)
exit_sub
end_if
' algorithme général
a0 = d / a
a1 = c / a
a2 = b / a
a3 = a2 / 3
p = a1 - a3 * a2
q = a0 - a1 * a3 + 2 * power(a3, 3)
delta = power(q / 2, 2) + power(p / 3, 3)
if delta > 0 : ' une racine réelle et deux racimes complexes
' calcul intermédiaire
w1 = 0-q/2 + sqr(delta)
w = sgn(w1) * power(abs(w1),1/3)
' les solutions sont
x1 = w - (p/3) / w - a3
x2 = 0-(a2 + x1) / 2
x3 = (sqr(3) / 2 * (w + (p / 3) /w))
' formatage des solutions
x1 = x1 + sgn(x1)*epsilon : x1 = int(x1*nbc+0.5)/nbc
x2 = x2 + sgn(x2)*epsilon : x2 = int(x2*nbc+0.5)/nbc
x3 = x3 + sgn(x3)*epsilon : x3 = int(x3*nbc+0.5)/nbc
item_add 40,"une racine réelle et deux racines complexes conjuguées"
item_add 40,"x1 = " + str$(x1)
if abs(x3) = 1 then i$ = "" : else : i$ = "*" + str$(abs(x3))
if abs(x3) < epsilon
item_add 40,"x2 = x2 = " + str$(x2)
else
item_add 40,"x2 = " + str$(x2) + " + i" + i$
item_add 40,"x3 = " + str$(x2) + " - i" + i$
exit_sub
end_if
end_if
if delta = 0 : ' p est nécessairement <= 0
if p = 0 : ' une racine réelle triple
x1 = 0-sgn(d/a)* power(abs(d/a),1/3) : ' x2 = x1 : x3 = x1
item_add 40,"Une racine réelle triple"
item_add 40,"x1 = x2 = x3 = " + str$(x1)
else : ' une racine simple et une racine double
x1 = 3*q/p : x1 = x1 - b/(3*a)
x2 = 0-3*q/(2*p) : x2 = x2- b/(3*a)
x3 = x2
' formatage des solutions
x1 = x1 + sgn(x1)*epsilon : x1 = int(x1*nbc+0.5)/nbc
x2 = x2 + sgn(x2)*epsilon : x2 = int(x2*nbc+0.5)/nbc
item_add 40,"Une racine réelle simple x1 = " + str$(x1)
item_add 40,"Une racine réelle double x2 = x3 = " + str$(x2)
end_if
else : ' delta < 0 donc 3 solutions réelles distinctes
' calculs intermédiaires
u = 2*sqr(0-p/3)
v = (0-q/2) / power((0-p/3),(3/2))
t = acos(v) / 3
' les 3 solutions
x1 = u * cos(t) - a3
x2 = u * cos(t+2*pi/3) - a3
x3 = u * cos(t+4*pi/3) - a3
' formatage des solutions
x1 = x1 + sgn(x1)*epsilon : x1 = int(x1*nbc+0.5)/nbc
x2 = x2 + sgn(x2)*epsilon : x2 = int(x2*nbc+0.5)/nbc
x3 = x3 + sgn(x3)*epsilon : x3 = int(x3*nbc+0.5)/nbc
item_add 40,"trois solutions réelles distinctes."
item_add 40,"x1 = " + str$(x1)
item_add 40,"x2 = " + str$(x2)
item_add 40,"x3 = " + str$(x3)
end_if
END_SUB
rem ============================================================================
SUB Degre_4()
dim_local a$,b$,c$,d$,e$
if text$(22) = "" or text$(24) = "" or text$(26) = "" or text$(26) = "" or text$(28) = ""
message "!!! Veuillez indiquer tous les coefficients !!!"
exit_sub
end_if
if numeric(text$(22)) = 0 or numeric(text$(24)) = 0 or numeric(text$(24)) = 0 or numeric(text$(26)) = 0 or numeric(text$(28)) = 0
message "!!! Veuillez indiquer des valeurs numériques pour les coefficients !!!"
exit_sub
end_if
a = val(text$(22))
if a = 0
message "!!! La valeur de a doit être différente de zéro !!!"
exit_sub
end_if
b = val(text$(24)) : c = val(text$(26)) : d = val(text$(28)) : e = val(text$(30))
if a = 1 then a$ = "x^4 " : else : a$ = str$(a) + "x^4 " : ' Pour ne pas afficher 1x³
if a = -1 then a$ = "-x^4 " : ' pour ne pas afficher -1x³
if b = 1 then b$ = "+x³ " : else : b$ = str$(b) + "x³ " : ' Pour ne pas afficher 1x³ =
if b = -1 then b$ = "-x³ " : ' pour ne pas afficher -1x³
if b > 1 then b$ = "+ " + str$(b) + "x³ "
if b = 0 then b$ = ""
if c = 1 then c$ = "+x² " : else : c$ = str$(c) + "x² " : ' pour ne pas afficher 1x²
if c = -1 then c$ = "-x² " : ' pour ne pas afficher -1x²
if c > 1 then c$ = "+ " + str$(c) + "x² "
if c = 0 then c$ = ""
if d = 1 then d$ = "+x " : else : d$ = str$(d) + "x "
if d = -1 then d$ = "-x "
if d > 1 then d$ = "+ " + str$(d) + "x "
if d = 0 then d$ = ""
if e = 0 then e$ = " = 0" : else : e$ = str$(e)+" = 0"
if e > 0 then e$ = "+ " + e$
item_add 40,"L'équation du quatrième degré"
item_add 40, a$+b$+c$+d$+e$
item_add 40, "admet comme solutions :"
Equat4(a,b,c,d,e)
END_SUB
rem ============================================================================
' Résolution de l'équation du 4ème degré ax^4 + bx³ + cx² + dx + e = 0
SUB Equat4(a,b,c,d,e)
passe = 0
' cas trivial
if b = 0 and c = 0 and d = 0 and e = 0
item_add 40,"Une racine multiple d'ordre 4"
item_add 40,"x1 = x2 = x3 = x4 = 0"
exit_sub
end_if
z = b/(2*a)
aa = c/a - 3*power(z,2)/2
bb = d/a + power(z,3) - c*z/a
cc = e/a - 3 * power(z/2,4) + c * power(z,2) / (4 * a) - d * z / (2*a)
d2 = -2 * power(aa,3) / 27 - power(bb,2) + 8 * aa * cc / 3
c2 = 0-(aa*aa + 12*cc) / 3
delta = power(c2/3,3) + power(d2/2,2)
' calculs intermédiares en fonction de delta
if delta > 0
w = power(0-d2/2 + sqr(delta),1/3)
u = w - c2 / (3*w)
end_if
if delta = 0
u = 3 * d2 / c2
end_if
if delta < 0
u = 2 * sqr(0-c2/3) * cos((1/3)*acos(0-d2 / (2 * power((0-c2/3),(3/2)))))
end_if
' autres calculs intermédiaires
t = aa / 3 + u
r = sqr(t-aa)
s = sqr((t/2)*(t/2) -cc)
decal = 0-b/(4*a)
' les 2 premières solutions sont données par :
' calculs intermédiaires :
delta = r*r - 2*t - 4*s
p1 = 0-r/2
Calculs_Intermediaires()
' les 2 autres solutions sont données par :
' calculs intermédiaires
delta = r*r -2 *t + 4 *s
p1 = r/2
Calculs_Intermediaires()
END_SUB
rem ============================================================================
SUB Calculs_Intermediaires()
passe = passe + 1
if bb > 0 then p1 = 0-p1
p2 = sqr(abs(delta)) / 2
if delta >= 0 : ' 2 solutions réelles
x1 = p1+p2+decal
x2 = p1-p2+decal
' formatage
x1 = x1 + sgn(x1)*epsilon : x1 = int(x1*nbc+0.5)/nbc
x2 = x2 + sgn(x2)*epsilon : x2 = int(x2*nbc+0.5)/nbc
if passe = 1
item_add 40,"x1 = " + str$(x1)
item_add 40,"x2 = " + str$(x2)
else
item_add 40,"x3 = " + str$(x1)
item_add 40,"x4 = " + str$(x2)
end_if
end_if
if delta < 0 : ' 2 solutions complexes
re = p1+decal
im = p2
re = re + sgn(re)*epsilon : re = int(re*nbc+0.5)/nbc
im = im + sgn(im)*epsilon : im = int(im*nbc+0.5)/nbc
if passe = 1
item_add 40,"x1 = " + str$(re) + " + i* " + str$(im)
item_add 40,"x2 = " + str$(re) + " - i* " + str$(im)
else
item_add 40,"x3 = " + str$(re) + " + i* " + str$(im)
item_add 40,"x4 = " + str$(re) + " - i* " + str$(im)
end_if
end_if
END_SUB
rem ============================================================================
Quitter:
if message_confirmation_yes_no("Vous voulez vraiment quitter ?") = 1
terminate
end_if
return
rem ============================================================================
- Spoiler:
- Spoiler:
Dernière édition par papydall le Ven 13 Mar 2020 - 13:40, édité 1 fois (Raison : Correction d'une coquille mentionnée par Marc) | |
|   | | Marc

Nombre de messages : 2466
Age : 63
Localisation : TOURS (37)
Date d'inscription : 17/03/2014
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Ven 13 Mar 2020 - 8:55 Ven 13 Mar 2020 - 8:55 | |
|  Merci et bravo Papydall ! Après plusieurs tests, je n'ai pas trouvé de faille  Merci pour le partage et bonne programmation à tous ! | |
|   | | Marc

Nombre de messages : 2466
Age : 63
Localisation : TOURS (37)
Date d'inscription : 17/03/2014
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Ven 13 Mar 2020 - 9:19 Ven 13 Mar 2020 - 9:19 | |
| Mince ! Un "n" s'est fait la malle sans aucune conséquence sur les calculs : 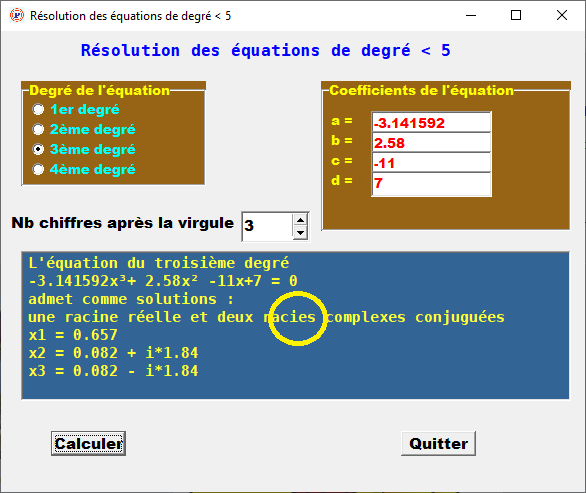 Je suis passé "dessus" plusieurs fois sans voir l'anomalie... comme quoi le cerveau humain a la faculté de corriger automatiquement certaines aberrations. EDIT : Bien que je n’ai ni la qualité, ni le niveau pour me permettre une critique, je dirais quand même : C’est un programme très bien conçu (comme d’habitude). Le source est très lisible avec de nombreux commentaires (comme d’habitude). Il embarque toute une batterie de vérifications et tests pour surveiller la saisie de l’utilisateur. Il est donc impossible de planter le programme. La présentation est d’un visuel très agréable et ergonomique. Donc, en conclusion, après avoir usurpé le titre et la fonction de professeur/correcteur/critique, j’attribue une appréciation TB avec les compliments du correcteur !      | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Ven 13 Mar 2020 - 13:42 Ven 13 Mar 2020 - 13:42 | |
| Bonjour tout le monde. Bonjour Marc. Merci beaucoup, Marc pour avoir tester mon programme et pour l’appréciation TB que tu m’as attribuée. - Marc a écrit:
- Mince ! Un "n" s'est fait la malle sans aucune conséquence sur les calculs :
Bon, je dirai une « naine » est passée tout juste devant moi sans l’avoir vue ! Je penserai à changer de lunettes. Sérieusement, je me suis donné à cœur joie pour blinder mon code contre les saisies fantaisistes de l’utilisateur étourdi ou qui cherche simplement les petites bêtes. Mais, on n’est jamais à l’abri d’une coquille, d’un oubli ou d’une chose à laquelle on n’y a pas pensé. NOTA : J’ai corrigé (ci-haut) la naine mentionnée par Marc | |
|   | | jjn4

Nombre de messages : 2747
Date d'inscription : 13/09/2009
 |  Sujet: +++ Sujet: +++  Ven 13 Mar 2020 - 14:55 Ven 13 Mar 2020 - 14:55 | |
| Ca, c'est du Papydall-Math++ ! Superbe, bravo !  | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Ven 13 Mar 2020 - 23:15 Ven 13 Mar 2020 - 23:15 | |
| Merci jjn4. Toi aussi tu fais des beaux jeux. Chacun son domaine et personne n'est parfait. Actuellement je suis sur un autre code (toujours dans les polynômes, mais ne dit rien à personne). Mon code avance d'une manière satisfaisante, sans trop de problèmes, mais lorsque ces inévitables problèmes se présenteront, je ferais une pause (et non une pose) pour aller jouer à l'un de tes superbes jeux, question de me ressourcer et d'éviter de donner un coup de poing à mon écran.  Hé oui ! Cette tentation m'arrive parfois, mais j'ai toujours su me retenir au bon moment!  Bon, je retourne à mes polynômes. Bonne nuit à tous! | |
|   | | jjn4

Nombre de messages : 2747
Date d'inscription : 13/09/2009
 |  Sujet: +++ Sujet: +++  Sam 14 Mar 2020 - 16:28 Sam 14 Mar 2020 - 16:28 | |
| Bonne programmation ! (hé, empêcher de casser la machine, voilà une utilisation des jeux à laquelle je n'avais pas pensé !  ) | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Sam 14 Mar 2020 - 16:59 Sam 14 Mar 2020 - 16:59 | |
| @jjn4
Tu peux télécharger sur mon webdav stress_reducers.zip
Défi : Tu peux faire un jeu pareil ou ressemblant ?
Bon, ce n'est pas trop difficile pour toi.
Et si ça te donne du fil à retordre, tu peux te déstresser avec stress_reduicers.exe | |
|   | | jjn4

Nombre de messages : 2747
Date d'inscription : 13/09/2009
 |  Sujet: +++ Sujet: +++  Dim 15 Mar 2020 - 17:16 Dim 15 Mar 2020 - 17:16 | |
| Ah, horreur ! Mon écran est tout cassé, taché, brûlé, cisaillé...  Heureusement, j'ai pu détruire ces sales termites qui bouffaient tout avec le pistolet laser !  | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Dim 15 Mar 2020 - 23:59 Dim 15 Mar 2020 - 23:59 | |
| Hé jjn4, tu dois préciser que ton « écran est tout cassé, taché, brûlé, cisaillé … » VIRTUELLEMENT et non dans la réalité. Sinon, on va croire que stress_reducers.exe est le coupable ! On n’est pas tous des Martiens, ici !!!    De toutes les façons, tu t'es bien défoulé en utilisant toutes les armes proposées, à ce que je vois. | |
|   | | jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Mer 1 Avr 2020 - 9:34 Mer 1 Avr 2020 - 9:34 | |
| J'ai placé sur mon WebDav un programme qui résout les équations polynomiales jusqu'au degré 20 Dossier Math, fichier polysolve.exe Les sources pour Delphi 7 sont dans ma bibliothèque DMath : https://sourceforge.net/projects/dmath/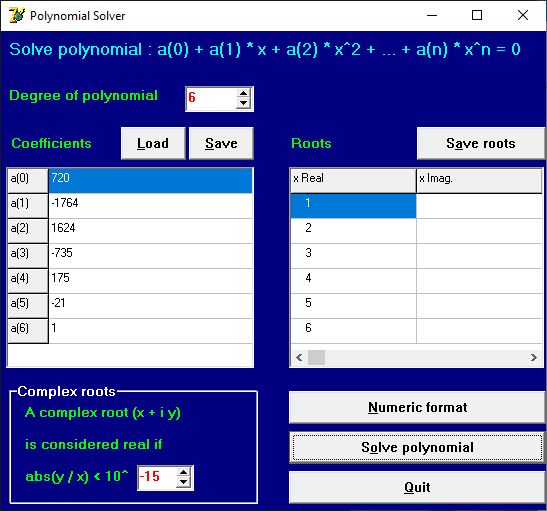 | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Dim 5 Avr 2020 - 0:13 Dim 5 Avr 2020 - 0:13 | |
| Merci Jean_Debord pour ce partage. Je suis actuellement en train de coder un programme en Panoramic qui, lui aussi résout les polynômes de degré quelconque (du degré 1 au degré 99 et plus si affinité) par la méthode de Bairstow. En réalité, mon programme se contentera de résoudre des polynômes de degré 1 à 20 (commodité de l’affichage sur écran), mais l’algorithme utilisé n’interdit pas les polynômes de degré supérieur. Je m’inspirerai de l’affichage de ton programme Polynomial Solver pour réaliser le mien. - ça donnerai quelque chose comme:
| |
|   | | jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Dim 5 Avr 2020 - 8:17 Dim 5 Avr 2020 - 8:17 | |
| Bonjour papydall. Merci de ton intérêt pour mon programme  Pour moi aussi la limite à 20 est arbitraire. On pourrait aller plus loin. L'algorithme calcule les valeurs propres de la matrice compagnon. | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  Dim 5 Avr 2020 - 9:00 Dim 5 Avr 2020 - 9:00 | |
| | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4 Sujet: Re: Résolution des équations polynomiales de degré 1, 2, 3 et 4  | |
| |
|   | | | | Résolution des équations polynomiales de degré 1, 2, 3 et 4 |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
