| Novembre 2024 | | Lun | Mar | Mer | Jeu | Ven | Sam | Dim |
|---|
| | | | | 1 | 2 | 3 | | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | 11 | 12 | 13 | 14 | 15 | 16 | 17 | | 18 | 19 | 20 | 21 | 22 | 23 | 24 | | 25 | 26 | 27 | 28 | 29 | 30 | |  Calendrier Calendrier |
|
|
| | La théorie du chaos |  |
| | | Auteur | Message |
|---|
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: La théorie du chaos Sujet: La théorie du chaos  Sam 8 Sep 2018 - 10:17 Sam 8 Sep 2018 - 10:17 | |
| Avec l'ensemble de Mandelbrot, la suite logistique, encore appelée "itérateur quadratique", constitue l'un des emblèmes de la théorie du chaos. Il s'agit d'une suite de nombres dépendant d'un paramètre. Pour les faibles valeurs de ce dernier, la suite tend vers une valeur unique. Lorsqu'on augmente le paramètre, la suite devient périodique, oscillant entre 2, puis 4, 8, 16 ... valeurs. Au-delà d'une valeur critique du paramètre la suite devient chaotique, mais il existe des zones de périodicité à l'intérieur du régime chaotique où l'on trouve des périodes impaires (3, 5, 7 ...) ainsi que leurs multiples par les puissances de 2 (2*3, 4*3, ... 2*5, 4*5, ...) Le programme suivant (pour FBPano) permet de visualiser le comportement de cette suite. Le graphique montre un exemple avec a = 3.5 : la période est égale à 4. - Code:
-
' ********************************************************************
' Itérateur quadratique : x(n + 1) = a * x(n) * [1 - x(n)]
' ********************************************************************
' Ce programme montre le comportement d'un système dynamique :
' l'itérateur quadratique (ou suite logistique).
'
' Ce système est défini par l'équation :
'
' x(n+1) = a.x(n).[1 - x(n)]
'
' Pour a < 3 la suite tend vers une valeur unique
'
' Pour a >= 3 la suite devient périodique, avec une cascade
' de doublements de période :
'
' a 3 3.5 3.55 3.566
' Période 2 4 8 16
'
' Le régime chaotique débute à partir de a ~ 3.57, avec toutefois des
' zones de comportement périodiques à l'intérieur de ce régime, p. ex.
'
' a 3.63 3.74 3.83
' Période 6 5 3
'
' On peut aussi observer une alternance de phases périodiques et
' chaotiques, phénomène connu sous le nom d'intermittence (p. ex.
' pour a = 3.82812)
'
' Pour plus d'informations, voir la page de Wikipédia :
' https://fr.wikipedia.org/wiki/Suite_logistique
' **********************************************************************
' --------------------------------------------------------------------
' Constantes et variables globales
' --------------------------------------------------------------------
const Nmax = 100, Nstep = 10 ' Echelle sur Ox (itérations)
const Xmin = 0, Xmax = 1, Xstep = 0.1 ' Echelle sur Oy (valeurs x(n))
const Npixels = 5 ' Nb de pixels par itération
const WCAN = Nmax * Npixels ' Largeur du CANVAS
const HCAN = 400 ' Hauteur du CANVAS
const Xfact = HCAN / (Xmax - Xmin) ' Facteur d'échelle
const Font = FL_HELVETICA, Size = 15 ' Police de caract. et taille
dim X(Nmax) ' Suite x(n)
' --------------------------------------------------------------------
' Construction de l'interface graphique
' --------------------------------------------------------------------
enum
frm, alf, edit1, edit2, btn, can, xalfx, xalfy
end_enum
form frm, 100, 100, WCAN + 110, HCAN + 210, "Itérateur quadratique"
alpha alf, 10, 10, WCAN + 90, 30, "x(n + 1) = a * x(n) * [1 - x(n)]", , FL_FLAT_BOX
edit edit1, 80, 50, 100, 30, "a [1..4] = ", , T_Edit_Float
edit edit2, 330, 50, 100, 30, "x(0) ]0..1[ = ", , T_Edit_Float
button btn, 500, 50, 100, 30, "Tracer"
xcanvas can, 90, 120, WCAN, HCAN
xalpha xalfx, 80, 130 + HCAN, WCAN + 30, 100
xalpha xalfy, 10, 110, 70, HCAN + 20
color_fl alf, FL_DARK_BLUE
color_caption_fl alf, FL_CYAN
font_caption alf, FL_HELVETICA_BOLD, 18
color_text_fl edit1, FL_RED
color_text_fl edit2, FL_RED
text edit1, "3.5"
text edit2, "0.5"
on_click btn, click_btn
on_draw xalfx, draw_xalfx
on_draw xalfy, draw_xalfy
on_canvas_draw can, draw_can
' --------------------------------------------------------------------
' Lancement de l'application
' --------------------------------------------------------------------
start 0
' --------------------------------------------------------------------
' Sous-programme auxiliaire
' --------------------------------------------------------------------
sub plot_point (i%, x)
' Marque le point pour l'itération i
dim ip%, xp%
ip = i * Npixels ' Abscisse du point en pixels
xp = HCAN - Xfact * (x - Xmin) ' Ordonnée du point en pixels
if i = 0 then
2d_move_to ip, xp
else
2d_line_to ip, xp
end_if
2d_pie ip, xp, 3
end_sub
' --------------------------------------------------------------------
' Sous-programmes associes aux evenements
' --------------------------------------------------------------------
function draw_xalfx% ()
' Tracé de l'axe Ox
dim x0%, y0%, w0%, h0%, x1%, xt%, yt%, wt%, ht%
dim i%, n%, stp, txt$
get_xywh xalfx, x0, y0, w0, h0
x1 = x0 + 10
2d_pen_color_fl FL_BLACK
2d_line_h x1, y0, x0 + w0 - 20
2d_font font, size
n = Nmax / Nstep
stp = (w0 - 30) / n
for i = 0 to n
txt = str(i * Nstep)
2d_line_v x1, y0, y0 + 10
2d_text_extension txt, xt, yt, wt, ht
2d_print txt, x1 - wt \ 2, y0 + 20 + ht
x1 = x1 + stp
next i
txt = "Itérations"
2d_text_extension txt, xt, yt, wt, ht
2d_print txt, x0 + (w0 - wt) \ 2, y0 + 60
draw_xalfx = 1
end_function
function draw_xalfy% ()
' Tracé de l'axe Oy
dim x0%, y0%, w0%, h0%, y1%, xt%, yt%, wt%, ht%
dim i%, n%, stp, txt$*4
get_xywh xalfy, x0, y0, w0, h0
y1 = y0 + 10
2d_pen_color_fl FL_BLACK
2d_line_v x0 + w0, y1, y0 + h0 - 10
2d_font font, size
n = (Xmax - Xmin) / Xstep
stp = HCAN / n
for i = 0 to n
sprintf txt, "%3.1f", Xmin + (n - i) * Xstep
2d_line_h x0 + w0, y1, x0 + w0 - 10
2d_text_extension txt, xt, yt, wt, ht
2d_print txt, x0 + w0 - 20 - wt, y1 + ht \ 2
y1 = y1 + stp
next i
txt = "x(n)"
2d_text_extension txt, xt, yt, wt, ht
2d_print txt, x0 + 10, y0 + 10 + wt + (h0 - wt) \ 2, 90
draw_xalfy = 1
end_function
sub draw_can()
' Tracé du diagramme
dim i%
2d_pen_color_fl FL_BLACK
2d_rectangle_fill 0, 0, WCAN, HCAN
2d_pen_color_fl FL_GREEN
for i = 1 to Nmax
plot_point i, X(i)
next i
end_sub
sub click_btn ()
' Calcul des itérations
dim a, i%
a = val(get_text(edit1))
if a < 1 or a > 4 then
message "a doit être entre 1 et 4"
exit_sub
end_if
X(0) = val(get_text(edit2))
if X(0) <= 0 or X(0) >= 1 then
message "x(0) doit être entre 0 et 1 (non compris)"
exit_sub
end_if
for i = 1 to Nmax
X(i) = a * X(i - 1) * (1 - X(i - 1))
next i
object_redraw can
end_sub
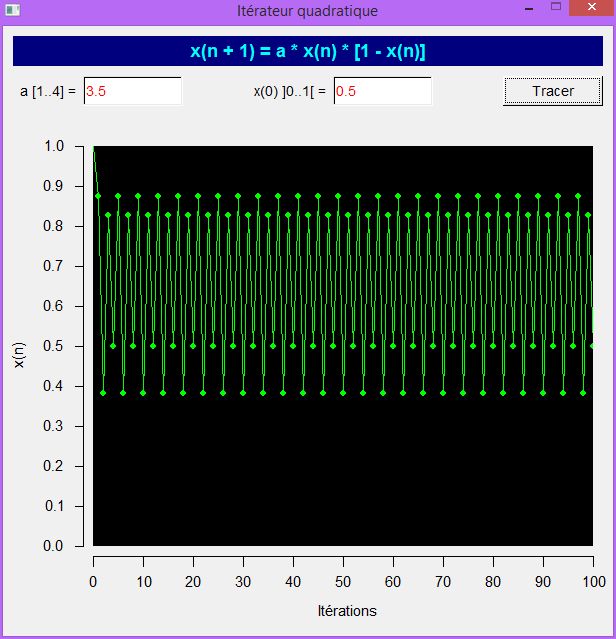 | |
|   | | jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: La théorie du chaos Sujet: Re: La théorie du chaos  Mar 11 Sep 2018 - 9:30 Mar 11 Sep 2018 - 9:30 | |
| Il n'est pas toujours facile de déterminer la période sur le diagramme des "orbites" (programme précédent). On peut s'aider du spectre de puissance, comme nous l'avons fait pour les sons (voir exemples\sound\test3.bas) Le programme suivant calcule ce spectre (vous pouvez récupérer les sous-programmes spectrum_coef et spectrum_power pour votre propre usage). Sur le graphique, on voit que la période est de 16 (on prend le plus grand nombre, les autres correspondent aux harmoniques). - Code:
-
' ********************************************************************
' Itérateur quadratique : Calcul du spectre de puissance
' ********************************************************************
' --------------------------------------------------------------------
' Constantes et variables globales
' --------------------------------------------------------------------
const Tmin = 2, Tmax = 20, Tstep = 1 ' Echelle sur Ox (périodes)
const dBmin = 0, dBmax = 200, dBstep = 20 ' Echelle sur Oy (décibels)
const Tfact = 30 ' Nb de pixels par période
const WCAN = (Tmax - Tmin) * Tfact ' Largeur du CANVAS
const HCAN = 400 ' Hauteur du CANVAS
const dBfact = HCAN / (dBmax - dBmin) ' Facteur d'échelle sur Oy
const font = FL_HELVETICA, size = 15 ' Police de caract. et taille
const Ncoef = 50 ' Nb de coefficients pour
' le calcul du spectre
dim P(WCAN) ' Puissances
' --------------------------------------------------------------------
' Construction de l'interface graphique
' --------------------------------------------------------------------
enum
frm, alf, edit1, edit2, spin1, spin2, btn, can, xalfx, xalfy
end_enum
form frm, 100, 100, WCAN + 100, HCAN + 250, "Itérateur quadratique : Spectre de puissance"
alpha alf, 10, 10, WCAN + 80, 30, "x(n + 1) = a * x(n) * [1 - x(n)]", , FL_FLAT_BOX
edit edit1, 90, 50, 100, 30, "a ]3..4[ = ", , T_Edit_Float
edit edit2, 90, 90, 100, 30, "x(0) ]0..1[ = ", , T_Edit_Float
spin spin1, 305, 50, 75, 30, "Calculer "
spin spin2, 555, 50, 75, 30, " points à partir du point n° "
button btn, 245, 90, 385, 30, "Calculer"
xcanvas can, 90, 160, WCAN, HCAN
xalpha xalfx, 80, 170 + HCAN, WCAN + 30, 100
xalpha xalfy, 10, 150, 70, HCAN + 20
color_fl alf, FL_DARK_BLUE
color_caption_fl alf, FL_CYAN
font_caption alf, FL_HELVETICA_BOLD, 18
dim obj%
for obj = edit1 to spin2
color_text_fl obj, FL_RED
next obj
text edit1, "3.566"
text edit2, "0.5"
position_range spin1, 1000, 10000, 1000
position_range spin2, 100, 1000, 100
position spin1, 1000
position spin2, 100
on_click btn, click_btn
on_draw xalfx, draw_xalfx
on_draw xalfy, draw_xalfy
on_canvas_draw can, draw_can
' --------------------------------------------------------------------
' Lancement de l'application
' --------------------------------------------------------------------
start 0
' --------------------------------------------------------------------
' Sous-programme auxiliaire
' --------------------------------------------------------------------
function y_pixel% (P)
' Calcule l'ordonnée pour une valeur de puissance
dim dB = 4.342944819032518 * log(P) ' 10 ln(P) / ln(10)
y_pixel = HCAN - dBfact * (dB - dBmin)
end_function
' --------------------------------------------------------------------
' Sous-programmes associes aux evenements
' --------------------------------------------------------------------
function draw_xalfx% ()
' Tracé de l'axe Ox
dim x0%, y0%, w0%, h0%, x1%, xt%, yt%, wt%, ht%
dim i%, n%, stp, txt$
get_xywh xalfx, x0, y0, w0, h0
x1 = x0 + 10
2d_pen_color_fl FL_BLACK
2d_line_h x1, y0, x0 + WCAN + 10
2d_font font, size
n = (Tmax - Tmin) / Tstep
stp = WCAN / n
for i = 0 to n
txt = str(Tmin + i * Tstep)
2d_line_v x1, y0, y0 + 10
2d_text_extension txt, xt, yt, wt, ht
2d_print txt, x1 - wt \ 2, y0 + 20 + ht
x1 = x1 + stp
next i
txt = "Période"
2d_text_extension txt, xt, yt, wt, ht
2d_print txt, x0 + (w0 - wt) \ 2, y0 + 60
draw_xalfx = 1
end_function
function draw_xalfy% ()
' Tracé de l'axe Oy
dim x0%, y0%, w0%, h0%, y1%, xt%, yt%, wt%, ht%
dim i%, n%, stp, txt$
get_xywh xalfy, x0, y0, w0, h0
y1 = y0 + 10
2d_pen_color_fl FL_BLACK
2d_line_v x0 + w0, y1, y0 + h0 - 10
2d_font font, size
n = (dBmax - dBmin) / dBstep
stp = HCAN / n
for i = 0 to n
txt = str((n - i) * dBstep)
2d_line_h x0 + w0, y1, x0 + w0 - 10
2d_text_extension txt, xt, yt, wt, ht
2d_print txt, x0 + w0 - 20 - wt, y1 + ht \ 2
y1 = y1 + stp
next i
txt = "Puissance relative (dB)"
2d_text_extension txt, xt, yt, wt, ht
2d_print txt, x0 + 10, y0 + 10 + wt + (h0 - wt) \ 2, 90
draw_xalfy = 1
end_function
sub draw_can()
' Tracé du spectre
dim i%
2d_pen_color_fl FL_BLACK
2d_rectangle_fill 0, 0, WCAN, HCAN
2d_pen_color_fl FL_GREEN
2d_move_to 1, y_pixel(P(1))
for i = 2 to WCAN
2d_line_to i, y_pixel(P(i))
next i
end_sub
sub click_btn ()
' Calcul du spectre de puissance
dim a, x0, n1%, n2%, i%, T, P0
a = val(get_text(edit1))
if a <= 3 or a >= 4 then
message "a doit être entre 3 et 4 (non compris)"
exit_sub
end_if
x0 = val (get_text(edit2))
if x0 <= 0 or x0 >= 1 then
message "x(0) doit être entre 0 et 1 (non compris)"
exit_sub
end_if
n1 = get_position(spin1)
n2 = get_position(spin2)
for i = 1 to n2
x0 = a * x0 * (1 - x0)
next i
dim x(n1), coef(Ncoef)
x(0) = x0
for i = 1 to n1
x(i) = a * x(i - 1) * (1 - x(i - 1))
next i
spectrum_coef x(), coef()
for i = 1 to WCAN
T = Tmin + i / Tfact
P(i) = spectrum_power(1 / T, 1, coef())
next i
P(0) = P(1)
P0 = min(P())
for i = 1 to WCAN
P(i) = P(i) / P0 ' Puissance relative
next i
object_redraw can
end_sub
' ------------------------------------------------------------
' Spectre de puissance
' D'après "Numerical Recipes"
' http://www.aip.de/groups/soe/local/numres/bookcpdf/c13-7.pdf
' ------------------------------------------------------------
sub spectrum_coef (x(), coef())
' Calcul des coefficients du spectre
' Entrée : x(1..np) = tableau des valeurs du signal (points équidistants)
' Sortie : coef(0..nc) = tableau des coefficients
dim np% = ubound(x)
dim nc% = ubound(coef)
dim wk1(np), wk2(np), wkm(nc)
dim i%, j%, k%, num, denom, s
s = 0
for i = 1 to np
s = s + x(i) * x(i)
next i
coef(0) = s / np
wk1(1) = x(1)
wk2(np - 1) = x(np)
for i = 2 to np - 1
wk1(i) = x(i)
wk2(i - 1) = x(i)
next i
for k = 1 to nc
num = 0
denom = 0
for i = 1 to np - k
num = num + wk1(i) * wk2(i)
denom = denom + wk1(i) * wk1(i) + wk2(i) * wk2(i)
next i
coef(k) = 2.0 * num / denom
coef(0) = coef(0) * (1.0 - coef(k) * coef(k))
if k > 1 then
for j = 1 to k - 1
coef(j) = wkm(j) - coef(k) * wkm(k - j)
next j
end_if
if k = ncoef then exit_for
for j = 1 to k
wkm(j) = coef(j)
next j
for i = 1 to np - k - 1
wk1(i) = wk1(i) - wkm(k) * wk2(i)
wk2(i) = wk2(i + 1) - wkm(k) * wk1(i + 1)
next i
next k
end_sub
function spectrum_power (f, dt, coef())
' Retourne la valeur de la puissance pour une fréquence f
' La fréquence est comprise entre 0 et N/2 où N est la fréquence d'échantillonnage
' dt est l'unité de temps = 1/N
const TwoPi = 6.28318530717959
dim k%, theta, wpr, wpi, wr, wi, sumi, sumr, wtemp
theta = TwoPi * f * dt
wpr = cos(theta)
wpi = sin(theta)
wr = 1.0
wi = 0.0
sumr = 1.0
sumi = 0.0
for k = 1 to ubound(coef)
wtemp = wr
wr = wr * wpr - wi * wpi
wi = wi * wpr + wtemp * wpi
sumr = sumr - coef(k) * wr
sumi = sumi - coef(k) * wi
next k
spectrum_power = coef(0) / (sumr * sumr + sumi * sumi)
end_function
 | |
|   | | | | La théorie du chaos |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
