| Novembre 2024 | | Lun | Mar | Mer | Jeu | Ven | Sam | Dim |
|---|
| | | | | 1 | 2 | 3 | | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | 11 | 12 | 13 | 14 | 15 | 16 | 17 | | 18 | 19 | 20 | 21 | 22 | 23 | 24 | | 25 | 26 | 27 | 28 | 29 | 30 | |  Calendrier Calendrier |
|
|
| | La Cigale et la Fourmi |  |
|
+4Francis-mr Jean Claude Minibug papydall 8 participants | |
| Auteur | Message |
|---|
jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Mer 9 Sep 2015 - 9:48 Mer 9 Sep 2015 - 9:48 | |
| Merci pour vos encouragements  Voici déjà la maison de la fourmi. Le sprite de droite correspond aux données du programme de Papydall. Les autres en sont déduits par rotation et changement d'échelle. 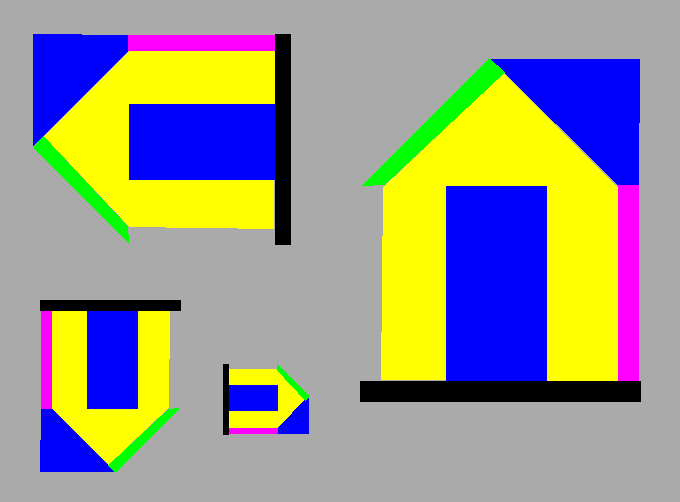 On pourra bien sûr stocker ces sprites dans des fichiers BMP ou dans des images en mémoire pour ensuite les placer où on veut. | |
|   | | jpcr

Nombre de messages : 276
Age : 57
Localisation : Val de Marne (94)
Date d'inscription : 06/05/2011
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Mer 9 Sep 2015 - 10:43 Mer 9 Sep 2015 - 10:43 | |
| cool  | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Mer 9 Sep 2015 - 11:51 Mer 9 Sep 2015 - 11:51 | |
| Bonjour tout le monde.
Madame Fourmi va passer l’hiver prochain bien au chaud et à l’abri des intempéries.
Je commence déjà à imaginer la pauvre Cigale !
Plus sérieusement, ça ouvre bien des horizons ces sprites.
Bonne continuation Jean. | |
|   | | Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Mer 9 Sep 2015 - 13:42 Mer 9 Sep 2015 - 13:42 | |
| Oui, quand l'ensemble des fonctions pour les sprites sera disponible, j'ai hâte de voir ce que donnera la reprise des programmes existant une fois compilé, au niveau des performances. | |
|   | | jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Jeu 10 Sep 2015 - 9:13 Jeu 10 Sep 2015 - 9:13 | |
| Avec les insectes j'obtiens des ... bugs ! (ce qui paraît logique ...)
La fourmi est beaucoup plus difficile à dessiner que sa maison. Il y a 12 polygones, ayant jusqu'à 49 sommets !
Je vais devoir un peu modifier tout ça ...
| |
|   | | Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Jeu 10 Sep 2015 - 10:25 Jeu 10 Sep 2015 - 10:25 | |
| A combattre sans péril on gagne sans gloire ...  | |
|   | | jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Ven 11 Sep 2015 - 8:59 Ven 11 Sep 2015 - 8:59 | |
| Oui mais j'avais sous-estimé l'adversaire  (ce qu'il ne faut jamais faire bien entendu ...) | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Sam 12 Sep 2015 - 3:59 Sam 12 Sep 2015 - 3:59 | |
| Un 'escargot' tracé avec des ''poly lignes '' dont les coordonnées se trouvent en lignes DATA. Il est possible de mémoriser ces coordonnées dans un tableau par exemple. On peut déplacer la figure. On peut modifier sa taille (agrandissement ou rapetissement). On peut lui faire subir une rotation d’un angle quelconque en degré dans le sens horaire ou dans le sens antihoraire. Bon, le résultat n’est pas un chef d’œuvre ! En plus le clignotement de l’affichage… Le but est de montrer la faisabilité de la chose, pas plus. - Code:
-
rem ============================================================================
rem Escargot
rem Par Papydall
rem ============================================================================
dim x,y,xo,yo,echelle,r,i
dim pi,rad ,newx,newy
pi = acos(-1) : rad = pi/180
xo = 0 : yo = 0 : echelle = 5 : r = .5
full_space 0 : 2d_fill_on : 2d_fill_color 0,0,0 : 2d_pen_width 3
alpha 10 : top 10,50 : left 10,200 : font_bold 10 : font_size 10,24
rem ============================================================================
' Appel : Escargot(xo,yo,echelle,tetha)
' xo,yo : Coordonnées de l'origine du tracé
' echelle : paramètre d'agrandissement / rappétissement de la figure
' tetha : angle en degré pour obtenir une rotation de la figure
' La rotation se fait
' dans le sens horaire pour tetha > 0
' dans le sens trigonometrique si tetha < 0
' Pour tetha = 0, il n'y a évidement pas de rotation
for i = 0 to 360 step 10
cls : Escargot(500,200,echelle,i) : pause 100 : ' rotation sens horaire
next i
for i = 0 to -360 step -10
cls : Escargot(500,200,echelle,i) : pause 100 : ' rotation sens anti-horaire
next i
Escargot(500,20,echelle/2,0) : pause 1000 : cls : ' échelle 1/2 pas de rotation
Escargot(500,20,echelle,0) : pause 1000 : cls : ' échelle normale pas de rotation
Escargot(500,20,echelle*2,0) : pause 1000 : cls : ' échelle double pas de rotation
Escargot(500,20,echelle*3,0) : pause 1000 : cls : ' échelle triple pas de rotation
for i = width(0) to -100*echelle step -2 : cls : Escargot(i,200,echelle*4,0) : pause 20 : next i
for i = height(0) to -100 step -2 : cls :Escargot(500,i,echelle,0) : pause 20 : next i
for i = -100 to height(0) step 2 : cls : Escargot(500,i,echelle,0) : pause 20:echelle = echelle*1.01:next i
caption 10,"That's all folks !!!"
for i = height(0) to 0 step -10: height 0,i : pause 100 : next i
terminate
end
rem ============================================================================
' Pour faire une rotation à un polygone, il faut faire la rotation à tous les
' sommets du polygone
SUB Escargot(xo,yo,echelle,tetha)
dim_local i,j,n
restore : read n : ' les cercles
for i = 1 to n
read x : read y
Rotation_Point(x,y,tetha) : 2d_circle xo + newx*echelle,yo + newy*echelle,r*echelle
next i
' La ligne
read x : read y : Rotation_Point(x,y,tetha) : 2d_poly_from xo + newx*echelle,yo + newy*echelle
read x : read y : Rotation_Point(x,y,tetha) : 2d_poly_to xo + newx*echelle,yo + newy*echelle
' Les polylignes
for j = 1 to 4
read x : read y :Rotation_Point(x,y,tetha) : 2d_poly_from xo + newx*echelle,yo + newy*echelle : read n
for i = 1 to n : read x : read y :Rotation_Point(x,y,tetha) : 2d_poly_to xo + newx*echelle,yo + newy*echelle : next i
next j
END_SUB
rem ============================================================================
' Rotation d'un point (x,y) d'un angle tetha en degrés.
' La rotation se fait
' dans le sens horaire pour tetha > 0
' dans le sens trigonometrique si tetha < 0
' Pour tetha = 0, il n'y a évidement pas de rotation
' Pour effectuer une rotation à un point il suffit de multiplier ses coordonnées
' par la matrice de rotation suivante :
' cos(tetha) -sin(tetha)
' sin(tetha) cos(tetha)
SUB Rotation_Point(x,y,tetha)
dim_local t
t = rad * tetha
newx = x * cos(t) - y * sin(t)
newy = x * sin(t) + y * cos(t)
END_SUB
rem ============================================================================
' cercles
data 6 : ' Nombre de cercles
data 1, 1, 9, 1, 3.5, 5, 6.5, 5, 1, 21, 9, 21
' ligne
data 0, 20, 30, 20
' Polyligne
data 1,1 : ' from
data 16 : ' Nombre de points
data 3,3, 1,5, 1,7, 3,9, 6,16, 9,19, 29,19, 27,17, 11,17, 7,9, 9,7, 9,5
data 7,3, 3,3, 7,3, 9,1
' Polyligne
data 3,7 : ' from
data 2 : ' Nombre de points
data 5,8, 7,7
' Polyligne
data 27,17 : ' from
data 6 : ' Nombre de points
data 29,13, 29,9, 25,5, 13,5, 9,9, 9,13
' Polyligne
data 15,17 : ' from
data 19 : ' Nombre de points
data 12,14, 12,9, 14,7, 24,7, 26,9, 26,13, 24,15, 16,15, 14,13, 14,10
data 15,8, 23,8, 24,9, 24,11, 23,12, 17,12, 16,11, 17,10, 21,10
rem ============================================================================
| |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Sam 12 Sep 2015 - 4:34 Sam 12 Sep 2015 - 4:34 | |
| En voici un autre, sur le même modèle. - Code:
-
rem ============================================================================
rem Ours
rem Par Papydall
rem ============================================================================
dim x,y,xo,yo,echelle,r,i
dim pi,rad ,newx,newy
pi = acos(-1) : rad = pi/180
xo = 0 : yo = 0 : echelle = 10 : r = .5
full_space 0 : 2d_fill_on : 2d_fill_color 0,0,0 : 2d_pen_width 5
alpha 10 : top 10,50 : left 10,200 : font_bold 10 : font_size 10,28
rem ============================================================================
' Appel : Ours(xo,yo,echelle,tetha)
' xo,yo : Coordonnées de l'origine du tracé
' echelle : paramètre d'agrandissement / rappétissement de la figure
' tetha : angle en degré pour obtenir une rotation de la figure
' La rotation se fait
' dans le sens horaire pour tetha > 0
' dans le sens trigonometrique si tetha < 0
' Pour tetha = 0, il n'y a évidement pas de rotation
for i = 0 to 2*pi step pi/4
x = width(0)/2 + 200*cos(i) : y = height(0)/2 + 200*sin(i)
Ours(x,y,echelle/2,i*180/pi)
next i
pause 2000
for i = 0 to 360 step 10
cls : Ours(500,300,echelle,i) : pause 100
next i
pause 1000
for i = 0 to -360 step -10
cls : Ours(500,300,echelle,i) : pause 100
next i
pause 1000 : cls
Ours(500,20,echelle/2,0) : pause 1000 : cls
Ours(500,20,echelle,0) : pause 1000 : cls
Ours(500,20,echelle*2,0) : pause 1000 : cls
Ours(500,20,echelle*3,0) : pause 1000 : cls
Ours(500,20,echelle*4,0) : pause 1000 : cls
for i = width(0) to -50*echelle step -5 : cls : Ours(i,200,echelle*2,0) : pause 20 : next i
for i = height(0) to -200 step -2 : cls : Ours(500,i,echelle,0) : pause 20 : next i
for i = -100 to height(0)-200 step 2
cls : Ours(500,i,echelle,0) : pause 20:echelle = echelle*1.01
next i
caption 10,"That's all folks !!!" : pause 200
for i = height(0) to 0 step -10: height 0,i : pause 100 : next i
terminate
end
rem ============================================================================
SUB Ours(xo,yo,echelle,tetha)
dim_local i,j,n
restore
for i = 1 to 2
read x : read y
Rotation_Point(x,y,tetha) : 2d_circle xo + newx*echelle,yo + newy*echelle,r*echelle
next i
for j = 1 to 9
read x : read y
Rotation_Point(x,y,tetha) : 2d_poly_from xo + newx*echelle,yo + newy*echelle : read n
for i = 1 to n
read x : read y
Rotation_Point(x,y,tetha) : 2d_poly_to xo + newx*echelle,yo + newy*echelle
next i
next j
END_SUB
rem ============================================================================
' Rotation d'un point (x,y) d'un angle tetha en degrés.
' La rotation se fait
' dans le sens horaire pour tetha > 0
' dans le sens trigonometrique si tetha < 0
' Pour tetha = 0, il n'y a évidement pas de rotation
' Pour effectuer une rotation à un point il suffit de multiplier ses coordonnées
' par la matrice de rotation suivante :
' cos(tetha) -sin(tetha)
' sin(tetha) cos(tetha)
SUB Rotation_Point(x,y,tetha)
dim_local t
t = rad * tetha
newx = x * cos(t) - y * sin(t)
newy = x * sin(t) + y * cos(t)
END_SUB
rem ============================================================================
' cercles
data 7.5, 9.5, 12.5, 9.5
' Polyligne
data 6,8 : ' from
data 3 : ' Nombre de points
data 7,7, 8,7, 9,8
' Polyligne
data 11,8 : ' from
data 3 : ' Nombre de points
data 12,7, 13,7, 14,8
' Polyligne
data 1,2 : ' from
data 28 : ' Nombre de points
data 1,4, 2,6, 4,7, 5,7, 4,9, 4,11, 6,15, 4,17, 8,19, 12,19,16,17, 14,15
data 16,11, 16,9, 15,7, 16,7, 18,6,19,4,19,2,17,1, 15,2, 13,4,12,3,8,3,7,4,5,2,3,1,1,2
' Polyligne
data 14,15 : ' from
data 3 : ' Nombre de points
data 12,16,8,16,6,15
' Polyligne
data 3,3 : ' from
data 5 : ' Nombre de points
data 3,4, 4,5,5,4,4,3,3,3
' Polyligne
data 16,3 : ' from
data 5 : ' Nombre de points
data 15,4,16,5,17,4,17,3,16,3
' Polyligne
data 9,11 : ' from
data 4 : ' Nombre de points
data 10,12, 11,11,10,10,9,11
' Polyligne
data 9,11 : ' from
data 8 : ' Nombre de points
data 7,11,6,13,8,15,10,14,12,15,14,13,13,11,11,11
' Polyligne
data 8,12: ' from
data 3 : ' Nombre de points
data 9,13,11,13,12,12
rem ============================================================================
| |
|   | | Minibug

Nombre de messages : 4570
Age : 58
Localisation : Vienne (86)
Date d'inscription : 09/02/2012
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Sam 12 Sep 2015 - 8:44 Sam 12 Sep 2015 - 8:44 | |
| Bonjour papydall ! L'idée est intéressante.  Pour ce qui est des déplacements en taille constante je pense qu'il est préférable de la transformer en image pour fluidifier le déplacement comme on l'a vu précédemment. Par contre je trouve l'idée de rotation très intéressante.
Dernière édition par Minibug le Sam 12 Sep 2015 - 10:53, édité 1 fois | |
|   | | jean_debord

Nombre de messages : 1266
Age : 70
Localisation : Limoges
Date d'inscription : 21/09/2008
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Sam 12 Sep 2015 - 9:13 Sam 12 Sep 2015 - 9:13 | |
| Merci Papydall pour ces nouveaux exemples "animaliers" ...
Mon système utilise aussi des DATA. Il subit toutefois les limitations de l'instruction DRAW de FreeBASIC. En particulier, on ne peut tracer que des polygones (pas de cercles) et le facteur d'échelle est exprimé en multiples du quart de la taille initiale (donc 1/4, 1/2, 3/4, etc.)
Avec FLTK on peut faire disparaître ces limitations en utilisant des matrices de transformations, comme tu le fais dans ton exemple. Je l'expliquerai dans un prochain article.
Pour le moment je m'en tiens aux instructions fournies par FreeBASIC. | |
|   | | Minibug

Nombre de messages : 4570
Age : 58
Localisation : Vienne (86)
Date d'inscription : 09/02/2012
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Sam 12 Sep 2015 - 13:29 Sam 12 Sep 2015 - 13:29 | |
| Voici une autre version de la fable de la fontaine qui va surement rappeler des souvenirs au plus anciens... La cigale et le fourmiPour les paroles c'est ici@Papydall : Désolé, c'est un peu hors sujet pour Panoramic, mais je n'ai pas pu m’empécher... Ok je sort...    | |
|   | | Jean Claude

Nombre de messages : 5950
Age : 70
Localisation : 83 Var
Date d'inscription : 07/05/2009
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Sam 12 Sep 2015 - 14:03 Sam 12 Sep 2015 - 14:03 | |
|
Dernière édition par Jean Claude le Sam 12 Sep 2015 - 20:50, édité 1 fois | |
|   | | Yannick
Nombre de messages : 8635
Age : 53
Localisation : Bretagne
Date d'inscription : 15/02/2010
 |  Sujet: re Sujet: re  Sam 12 Sep 2015 - 19:04 Sam 12 Sep 2015 - 19:04 | |
| Salut les poètes !... C' est bien beau tout çà mais personne ne fait rien pour cette pauvre cigale...  | |
|   | | Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Sam 12 Sep 2015 - 20:26 Sam 12 Sep 2015 - 20:26 | |
| D'abord bravo Panoramic pour tes programmes et tes procédures qui fonctionnent duper bien. A quand le prochain jeu vectoriel ? En tout cas tu peux faire un joli petit article avec ça. Sinon pour limiter le clignotement, tu peux simplement utiliser la méthode Silverman. Pour l'escargot ça donne ça: - Code:
- Code:
-
rem ============================================================================
rem Escargot
rem Par Papydall
rem ============================================================================
dim x,y,xo,yo,echelle,r,i, h
dim pi,rad ,newx,newy
pi = acos(-1) : rad = pi/180
xo = 0 : yo = 0 : echelle = 5 : r = .5
full_space 0 : 2d_fill_on : 2d_fill_color 0,0,0 : 2d_pen_width 3
image 4
picture 2 : width 2 ,width(0) : height 2,height(0): hide 2 : 2d_target_is 2
h = height(0) : height 0, 0
alpha 10 : top 10,50 : left 10,200 : font_bold 10 : font_size 10,24
rem ============================================================================
' Appel : Escargot(xo,yo,echelle,tetha)
' xo,yo : Coordonnées de l'origine du tracé
' echelle : paramètre d'agrandissement / rappétissement de la figure
' tetha : angle en degré pour obtenir une rotation de la figure
' La rotation se fait
' dans le sens horaire pour tetha > 0
' dans le sens trigonometrique si tetha < 0
' Pour tetha = 0, il n'y a évidement pas de rotation
for i = 0 to h step 10: height 0,i : pause 20 :next i
for i = 0 to 360 step 10
cls : Escargot(500,200,echelle,i) : pause 20 : copy_image() : ' rotation sens horaire
next i
for i = 0 to -360 step -10
cls : Escargot(500,200,echelle,i) : pause 20 : copy_image() : ' rotation sens anti-horaire
next i
cls : Escargot(500,20,echelle / 2,0) : pause 200 : copy_image() : ' échelle 1/2 pas de rotation
cls : Escargot(500,20,echelle,0) : pause 200 : copy_image() : ' échelle normale pas de rotation
cls : Escargot(500,20,echelle * 2,0) : pause 200 : copy_image() : ' échelle double pas de rotation
cls : Escargot(500,20,echelle * 3,0) : pause 200 : copy_image() : ' échelle triple pas de rotation
for i = width(0) to -100 * echelle step -5 : cls : Escargot(i,200,echelle*4,0) : pause 20 : copy_image() :next i
for i = height(0) to -100 step -4 : cls : Escargot(500,i,echelle,0) : pause 20 : copy_image() : next i
for i = -100 to height(0) step 4 : cls : Escargot(500,i,echelle,0) : pause 20: echelle = echelle*1.01: copy_image() :next i
caption 10,"That's all folks !!!"
for i = height(0) to 0 step -10: height 0,i : pause 20 :next i
terminate
end
rem ============================================================================
' Pour faire une rotation à un polygone, il faut faire la rotation à tous les
' sommets du polygone
SUB Escargot(xo,yo,echelle,tetha)
dim_local i,j,n
restore : read n : ' les cercles
for i = 1 to n
read x : read y
Rotation_Point(x,y,tetha) : 2d_circle xo + newx*echelle,yo + newy*echelle,r*echelle
next i
' La ligne
read x : read y : Rotation_Point(x,y,tetha) : 2d_poly_from xo + newx*echelle,yo + newy*echelle
read x : read y : Rotation_Point(x,y,tetha) : 2d_poly_to xo + newx*echelle,yo + newy*echelle
' Les polylignes
for j = 1 to 4
read x : read y :Rotation_Point(x,y,tetha) : 2d_poly_from xo + newx*echelle,yo + newy*echelle : read n
for i = 1 to n : read x : read y :Rotation_Point(x,y,tetha) : 2d_poly_to xo + newx*echelle,yo + newy*echelle : next i
next j
END_SUB
rem ============================================================================
' Rotation d'un point (x,y) d'un angle tetha en degrés.
' La rotation se fait
' dans le sens horaire pour tetha > 0
' dans le sens trigonometrique si tetha < 0
' Pour tetha = 0, il n'y a évidement pas de rotation
' Pour effectuer une rotation à un point il suffit de multiplier ses coordonnées
' par la matrice de rotation suivante :
' cos(tetha) -sin(tetha)
' sin(tetha) cos(tetha)
SUB Rotation_Point(x,y,tetha)
dim_local t
t = rad * tetha
newx = x * cos(t) - y * sin(t)
newy = x * sin(t) + y * cos(t)
END_SUB
rem ============================================================================
' cercles
data 6 : ' Nombre de cercles
data 1, 1, 9, 1, 3.5, 5, 6.5, 5, 1, 21, 9, 21
' ligne
data 0, 20, 30, 20
' Polyligne
data 1,1 : ' from
data 16 : ' Nombre de points
data 3,3, 1,5, 1,7, 3,9, 6,16, 9,19, 29,19, 27,17, 11,17, 7,9, 9,7, 9,5
data 7,3, 3,3, 7,3, 9,1
' Polyligne
data 3,7 : ' from
data 2 : ' Nombre de points
data 5,8, 7,7
' Polyligne
data 27,17 : ' from
data 6 : ' Nombre de points
data 29,13, 29,9, 25,5, 13,5, 9,9, 9,13
' Polyligne
data 15,17 : ' from
data 19 : ' Nombre de points
data 12,14, 12,9, 14,7, 24,7, 26,9, 26,13, 24,15, 16,15, 14,13, 14,10
data 15,8, 23,8, 24,9, 24,11, 23,12, 17,12, 16,11, 17,10, 21,10
rem ============================================================================
sub copy_image()
2d_image_copy 4,left(2),top(2),width(2),height(2)
2d_target_is 0: 2d_image_paste 4,left(2),top(2) : ' on recopie sur la fenêtre
2d_target_is 2
end_sub
| |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Sam 12 Sep 2015 - 22:26 Sam 12 Sep 2015 - 22:26 | |
| - jicehel a écrit:
- D'abord bravo Panoramic pour tes programmes et tes procédures qui fonctionnent duper bien
Moi également je dis bravo à Panoramic, car ses programmes et ses procédures fonctionnent duper bien.  Pour que tout fonctionne duper bien, il faut déplacer - Code:
-
2d_fill_on : 2d_fill_color 0,0,0 : 2d_pen_width 3 Juste après avoir déclaré - Code:
-
picture 2 : width 2 ,width(0) : height 2,height(0): hide 2 : 2d_target_is 2
h = height(0) : height 0, 0 pour que ces commandes soient prises en considération. A+ | |
|   | | Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Dim 13 Sep 2015 - 0:43 Dim 13 Sep 2015 - 0:43 | |
| OK, tu as raison, ça m'avait échappé. Du coup j'ai refais quelques ajustements ça donne - Code:
- Code:
-
rem ============================================================================
rem Escargot
rem Par Papydall
rem ============================================================================
dim x,y,xo,yo,echelle,r,i, h
dim pi,rad ,newx,newy
pi = acos(-1) : rad = pi/180
xo = 0 : yo = 0 : echelle = 5 : r = .5
full_space 0 : color 0,255,255,255
image 4
picture 2 : width 2 ,width(0) : height 2,height(0): hide 2 : 2d_target_is 2
h = height(0) : height 0, 0 : 2d_fill_on : 2d_fill_color 0,0,0 : 2d_pen_width 3
alpha 10 : top 10,50 : left 10,200 : font_bold 10 : font_size 10,24 : color 10,255,255,255
rem ============================================================================
' Appel : Escargot(xo,yo,echelle,tetha)
' xo,yo : Coordonnées de l'origine du tracé
' echelle : paramètre d'agrandissement / rappétissement de la figure
' tetha : angle en degré pour obtenir une rotation de la figure
' La rotation se fait
' dans le sens horaire pour tetha > 0
' dans le sens trigonometrique si tetha < 0
' Pour tetha = 0, il n'y a évidement pas de rotation
for i = 0 to h step 10: height 0,i : pause 20 :next i
for i = 0 to 360 step 10
cls : Escargot(500,200,echelle,i) : pause 20 : copy_image() : ' rotation sens horaire
next i
for i = 0 to -360 step -10
cls : Escargot(500,200,echelle,i) : pause 20 : copy_image() : ' rotation sens anti-horaire
next i
cls : Escargot(500,20,echelle / 2,0) : pause 200 : copy_image() : ' échelle 1/2 pas de rotation
cls : Escargot(500,20,echelle,0) : pause 200 : copy_image() : ' échelle normale pas de rotation
cls : Escargot(500,20,echelle * 2,0) : pause 200 : copy_image() : ' échelle double pas de rotation
cls : Escargot(500,20,echelle * 3,0) : pause 200 : copy_image() : ' échelle triple pas de rotation
pause 1000
for i = width(0) to -100 * echelle step -3 : cls : Escargot(i,200,echelle*4,0) : copy_image() :next i
for i = height(0) to -100 step -2 : cls : Escargot(500,i,echelle,0) : copy_image() : next i
for i = -100 to height(0) step 3 : cls : Escargot(500,i,echelle,0) : echelle = echelle*1.01: copy_image() :next i
2d_target_is 0 : cls : caption 10,"That's all folks !!!"
for i = height(0) to 0 step -10: height 0,i : pause 20 :next i
terminate
end
rem ============================================================================
' Pour faire une rotation à un polygone, il faut faire la rotation à tous les
' sommets du polygone
SUB Escargot(xo,yo,echelle,tetha)
dim_local i,j,n
restore : read n : ' les cercles
for i = 1 to n
read x : read y
Rotation_Point(x,y,tetha) : 2d_circle xo + newx*echelle,yo + newy*echelle,r*echelle
next i
' La ligne
read x : read y : Rotation_Point(x,y,tetha) : 2d_poly_from xo + newx*echelle,yo + newy*echelle
read x : read y : Rotation_Point(x,y,tetha) : 2d_poly_to xo + newx*echelle,yo + newy*echelle
' Les polylignes
for j = 1 to 4
read x : read y :Rotation_Point(x,y,tetha) : 2d_poly_from xo + newx*echelle,yo + newy*echelle : read n
for i = 1 to n : read x : read y :Rotation_Point(x,y,tetha) : 2d_poly_to xo + newx*echelle,yo + newy*echelle : next i
next j
END_SUB
rem ============================================================================
' Rotation d'un point (x,y) d'un angle tetha en degrés.
' La rotation se fait
' dans le sens horaire pour tetha > 0
' dans le sens trigonometrique si tetha < 0
' Pour tetha = 0, il n'y a évidement pas de rotation
' Pour effectuer une rotation à un point il suffit de multiplier ses coordonnées
' par la matrice de rotation suivante :
' cos(tetha) -sin(tetha)
' sin(tetha) cos(tetha)
SUB Rotation_Point(x,y,tetha)
dim_local t
t = rad * tetha
newx = x * cos(t) - y * sin(t)
newy = x * sin(t) + y * cos(t)
END_SUB
rem ============================================================================
' cercles
data 6 : ' Nombre de cercles
data 1, 1, 9, 1, 3.5, 5, 6.5, 5, 1, 21, 9, 21
' ligne
data 0, 20, 30, 20
' Polyligne
data 1,1 : ' from
data 16 : ' Nombre de points
data 3,3, 1,5, 1,7, 3,9, 6,16, 9,19, 29,19, 27,17, 11,17, 7,9, 9,7, 9,5
data 7,3, 3,3, 7,3, 9,1
' Polyligne
data 3,7 : ' from
data 2 : ' Nombre de points
data 5,8, 7,7
' Polyligne
data 27,17 : ' from
data 6 : ' Nombre de points
data 29,13, 29,9, 25,5, 13,5, 9,9, 9,13
' Polyligne
data 15,17 : ' from
data 19 : ' Nombre de points
data 12,14, 12,9, 14,7, 24,7, 26,9, 26,13, 24,15, 16,15, 14,13, 14,10
data 15,8, 23,8, 24,9, 24,11, 23,12, 17,12, 16,11, 17,10, 21,10
rem ============================================================================
sub copy_image()
2d_image_copy 4,left(2),top(2),width(2),height(2)
2d_target_is 0: 2d_image_paste 4,left(2),top(2) : ' on recopie sur la fenêtre
2d_target_is 2
end_sub
et du coup je mets aussi le code modifié de l'Ours. - Code de l'Ours:
- Code:
-
rem ============================================================================
rem Ours
rem Par Papydall
rem ============================================================================
dim x,y,xo,yo,echelle,r,i,h
dim pi,rad ,newx,newy
pi = acos(-1) : rad = pi/180
xo = 0 : yo = 0 : echelle = 10 : r = .5
full_space 0 : color 0,255,255,255
image 4
picture 2 : width 2 ,width(0) : height 2,height(0): hide 2 : 2d_target_is 2
h = height(0) : height 0, 0 : 2d_fill_on : 2d_fill_color 0,0,0 : 2d_pen_width 3
alpha 10 : top 10,50 : left 10,200 : font_bold 10 : font_size 10,24 : color 10,255,255,255
rem ============================================================================
' Appel : Ours(xo,yo,echelle,tetha)
' xo,yo : Coordonnées de l'origine du tracé
' echelle : paramètre d'agrandissement / rappétissement de la figure
' tetha : angle en degré pour obtenir une rotation de la figure
' La rotation se fait
' dans le sens horaire pour tetha > 0
' dans le sens trigonometrique si tetha < 0
' Pour tetha = 0, il n'y a évidement pas de rotation
for i = 0 to h step 10: height 0,i : pause 20 :next i
for i = 0 to 2*pi step pi/16
cls : x = width(0)/2 + 200*cos(i) : y = height(0)/2 + 200*sin(i)
Ours(x,y,echelle/2,i*180/pi) : copy_image() : pause 20
next i
pause 2000
for i = 0 to 360 step 10
cls : Ours(500,300,echelle,i) : copy_image(): pause 20
next i
pause 1000
for i = 0 to -360 step -10
cls : Ours(500,300,echelle,i) : copy_image(): pause 20
next i
pause 1000 : cls
cls : Ours(500,20,echelle/2,0) : pause 500: copy_image()
cls : Ours(500,20,echelle,0) : pause 500: copy_image()
cls : Ours(500,20,echelle*2,0) : pause 500: copy_image()
cls : Ours(500,20,echelle*3,0) : pause 500: copy_image()
cls : Ours(500,20,echelle*4,0) : pause 500: copy_image()
for i = width(0) to -50*echelle step -5 : cls : Ours(i,200,echelle*2,0) : pause 20: copy_image() : next i
for i = height(0) to -200 step -2 : cls : Ours(500,i,echelle,0) : pause 20 : copy_image(): next i
for i = -100 to height(0)-200 step 2 : cls : Ours(500,i,echelle,0) : pause 20:echelle = echelle*1.01 : copy_image() : next i
2d_target_is 0 : cls :caption 10,"That's all folks !!!" : pause 200
for i = height(0) to 0 step -10: height 0,i : pause 20 : next i
terminate
end
rem ============================================================================
SUB Ours(xo,yo,echelle,tetha)
dim_local i,j,n
restore
for i = 1 to 2
read x : read y
Rotation_Point(x,y,tetha) : 2d_circle xo + newx*echelle,yo + newy*echelle,r*echelle
next i
for j = 1 to 9
read x : read y
Rotation_Point(x,y,tetha) : 2d_poly_from xo + newx*echelle,yo + newy*echelle : read n
for i = 1 to n
read x : read y
Rotation_Point(x,y,tetha) : 2d_poly_to xo + newx*echelle,yo + newy*echelle
next i
next j
END_SUB
rem ============================================================================
' Rotation d'un point (x,y) d'un angle tetha en degrés.
' La rotation se fait
' dans le sens horaire pour tetha > 0
' dans le sens trigonometrique si tetha < 0
' Pour tetha = 0, il n'y a évidement pas de rotation
' Pour effectuer une rotation à un point il suffit de multiplier ses coordonnées
' par la matrice de rotation suivante :
' cos(tetha) -sin(tetha)
' sin(tetha) cos(tetha)
SUB Rotation_Point(x,y,tetha)
dim_local t
t = rad * tetha
newx = x * cos(t) - y * sin(t)
newy = x * sin(t) + y * cos(t)
END_SUB
rem ============================================================================
' cercles
data 7.5, 9.5, 12.5, 9.5
' Polyligne
data 6,8 : ' from
data 3 : ' Nombre de points
data 7,7, 8,7, 9,8
' Polyligne
data 11,8 : ' from
data 3 : ' Nombre de points
data 12,7, 13,7, 14,8
' Polyligne
data 1,2 : ' from
data 28 : ' Nombre de points
data 1,4, 2,6, 4,7, 5,7, 4,9, 4,11, 6,15, 4,17, 8,19, 12,19,16,17, 14,15
data 16,11, 16,9, 15,7, 16,7, 18,6,19,4,19,2,17,1, 15,2, 13,4,12,3,8,3,7,4,5,2,3,1,1,2
' Polyligne
data 14,15 : ' from
data 3 : ' Nombre de points
data 12,16,8,16,6,15
' Polyligne
data 3,3 : ' from
data 5 : ' Nombre de points
data 3,4, 4,5,5,4,4,3,3,3
' Polyligne
data 16,3 : ' from
data 5 : ' Nombre de points
data 15,4,16,5,17,4,17,3,16,3
' Polyligne
data 9,11 : ' from
data 4 : ' Nombre de points
data 10,12, 11,11,10,10,9,11
' Polyligne
data 9,11 : ' from
data 8 : ' Nombre de points
data 7,11,6,13,8,15,10,14,12,15,14,13,13,11,11,11
' Polyligne
data 8,12: ' from
data 3 : ' Nombre de points
data 9,13,11,13,12,12
rem ============================================================================
sub copy_image()
2d_image_copy 4,left(2),top(2),width(2),height(2)
2d_target_is 0: 2d_image_paste 4,left(2),top(2) : ' on recopie sur la fenêtre
2d_target_is 2
end_sub
Bon, plus qu'à dessiner une voiture ou une météorite et à utiliser cette technique pour faire une course de voiture ou un bon vieux "asteroid" | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Dim 13 Sep 2015 - 5:08 Dim 13 Sep 2015 - 5:08 | |
| Loin de la cigale, très loin de la fourmi, voici un personnage en couleurs ! - Code:
-
rem ============================================================================
rem Personnage
rem Par Papydall
rem ============================================================================
dim x,y,xo,yo,newx,newy,echelle,r,i,j,h
dim pi,rad : pi = acos(-1) : rad = pi/180
xo = 0 : yo = 0 : echelle = 10 : r = .4
full_space 0
picture 2 : width 2 ,width(0) : height 2,height(0): hide 2 : 2d_target_is 2
h = height(0) : height 0, 0
image 4
alpha 10 : top 10,50 : left 10,200 : font_bold 10 : font_size 10,24 : color 10,255,255,255
rem ============================================================================
for i = 0 to h step 10 : height 0,i : pause 20 : next i
for j = 1 to 2
for i = .5 to 6 step .25
cls : x = width(0)/3 : y = height(0)/2
Personnage(x,y,echelle*i,0+i*60) : copy_image() : pause 100
next i
for i = 6 to 0 step -.1
cls : x = width(0)/3 : y = 100
Personnage(x,y,echelle*i,0) : copy_image() : pause 20
next i
next j
2d_target_is 0 : cls :caption 10,"Bye Bye !!!" : pause 2000
for i = height(0) to 0 step -10: height 0,i : pause 20 : next i
terminate
end
rem ============================================================================
SUB Personnage(xo,yo,echelle,tetha)
dim_local i,j,n
restore
2d_fill_on : 2d_fill_color 255,0,0 : 2d_pen_width 3
for i = 1 to 2
read x : read y
Rotation_Point(x,y,tetha) : 2d_circle xo + newx*echelle,yo + newy*echelle,r*echelle
next i
for j = 1 to 18
read x : read y
Rotation_Point(x,y,tetha) : 2d_poly_from xo + newx*echelle,yo + newy*echelle : read n
for i = 1 to n
read x : read y
Rotation_Point(x,y,tetha) : 2d_poly_to xo + newx*echelle,yo + newy*echelle
next i
next j
x = 2 : y = 10 : Rotation_Point(x,y,tetha) : 2d_flood xo + newx*echelle,yo + newy*echelle,250,000,150
x = 8.5 : y = 9.5 : Rotation_Point(x,y,tetha) : 2d_flood xo + newx*echelle,yo + newy*echelle,255,250,000
x = 4 : y = 12.5 : Rotation_Point(x,y,tetha) : 2d_flood xo + newx*echelle,yo + newy*echelle,000,000,255
x = 5 : y = 14.5 : Rotation_Point(x,y,tetha) : 2d_flood xo + newx*echelle,yo + newy*echelle,100,050,010
x = 7 : y = 14.5 : Rotation_Point(x,y,tetha) : 2d_flood xo + newx*echelle,yo + newy*echelle,100,050,100
x = 3 : y = 3 : Rotation_Point(x,y,tetha) : 2d_flood xo + newx*echelle,yo + newy*echelle,000,255,000
x = 4 : y = 5 : Rotation_Point(x,y,tetha) : 2d_flood xo + newx*echelle,yo + newy*echelle,100,000,100
x = 8 : y = 5 : Rotation_Point(x,y,tetha) : 2d_flood xo + newx*echelle,yo + newy*echelle,100,000,100
END_SUB
rem ============================================================================
SUB Rotation_Point(x,y,tetha)
dim_local t
t = rad * tetha
newx = x * cos(t) - y * sin(t) : newy = x * sin(t) + y * cos(t)
END_SUB
rem ============================================================================
SUB Copy_Image()
2d_image_copy 4,left(2),top(2),width(2),height(2)
2d_target_is 0: 2d_image_paste 4,left(2),top(2)
2d_target_is 2
END_SUB
rem ============================================================================
data 5,6, 7,6
data 5,1
data 12
data 3,2 ,2,4, 2,6, 3,8, 5,9, 7,9, 9,8, 10,6, 10,4, 9,2, 7,1, 5,1
data 5,4
data 2
data 6,5, 7,4
data 3,4
data 10
data 3,5, 4,7, 5,7, 8,4, 9,4, 9,5, 8,7, 7,7, 4,4, 3,4
data 5.8, 7.2
data 2
data 6,7, 6.2,7.2
data 5,8
data 1
data 7,8
data 3,8
data 13
data 2,8, 1,9, 1,14, 2,14, 2,11, 3,12, 9,12, 10,11, 10,14, 11,14, 11,9, 10,8, 9,8
data 8,9
data 4
data 8,10, 9,10, 9,9, 8,9
data 3,12
data 3
data 3,13, 9,13, 9,12
data 5,13
data 5
data 5,14, 3,15, 9,15, 7,14, 7,13
data 6,13
data 1
data 6,15
data 1,13
data 1
data 2,13
data 10,13
data 1
data 11,13
data 1.25,14
data 1
data 1.25,13.50
data 1.50,14
data 1
data 1.50,13.50
data 1.75,14
data 1
data 1.75,13.50
data 10.25,14
data 1
data 10.25,13.50
data 10.50,14
data 1
data 10.50,13.50
data 10.75,14
data 1
data 10.75,13.50
rem ============================================================================
| |
|   | | Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Dim 13 Sep 2015 - 7:59 Dim 13 Sep 2015 - 7:59 | |
| Ca le fait  | |
|   | | Jean Claude

Nombre de messages : 5950
Age : 70
Localisation : 83 Var
Date d'inscription : 07/05/2009
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  Dim 13 Sep 2015 - 9:26 Dim 13 Sep 2015 - 9:26 | |
| Salut Il n'a pas l'air de bon poil ce personnage.  A+ | |
|   | | Contenu sponsorisé
 |  Sujet: Re: La Cigale et la Fourmi Sujet: Re: La Cigale et la Fourmi  | |
| |
|   | | | | La Cigale et la Fourmi |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
