| Novembre 2024 | | Lun | Mar | Mer | Jeu | Ven | Sam | Dim |
|---|
| | | | | 1 | 2 | 3 | | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | 11 | 12 | 13 | 14 | 15 | 16 | 17 | | 18 | 19 | 20 | 21 | 22 | 23 | 24 | | 25 | 26 | 27 | 28 | 29 | 30 | |  Calendrier Calendrier |
|
|
| | Rotation d'un point autour de l'origine |  |
| | | Auteur | Message |
|---|
papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Rotation d'un point autour de l'origine Sujet: Rotation d'un point autour de l'origine  Mar 1 Mar 2022 - 21:22 Mar 1 Mar 2022 - 21:22 | |
| - Code:
-
rem ============================================================================
rem Rotation d’un point
rem ============================================================================
rem Matrice de rotation d’un point P(x,y) d’un angle phi en degré.
rem Pour le point P(x,y) on applique la matrice de rotation suivante :
rem _ _ _ _ _ _
rem | | | | | |
rem | x’ | | cos(phi) -sin(phi) | | x |
rem | | = | | * | |
rem | y’ | | sin(phi) cos(phi) | | y |
rem |_ _| |_ _| |_ _|
rem
rem Ce qui donne le point P’(x’,y’) :
rem
rem
rem x’ = x * cos(phi) - y * sin(phi)
rem
rem y’ = y * cos(phi) + x * sin(phi)
rem
rem
rem ============================================================================
rem Info:
rem Pour faire tourner une figure, il suffit de faire tourner tous les points
rem qui définissent cette figure.
rem ============================================================================
dim x,y,xprime,yprime,x0,y0,phi
picture 10 : full_space 10 : 2d_target_is 10 : print_target_is 10 : font_bold 10
caption 0,"Rotation d'un point P(x,y) ----> P'(x',y')"
x0 = width_client(10)/2 : y0 = height_client(10)/2
degrees : ' On travaille en degré
2d_line 0,y0,2*x0,y0 : ' axe des x
2d_line x0,0,x0,2*y0 : ' axe des y
x = 150 : y = 60 : ' coordonnées du point qui subira la rotation
2d_pen_color 0,0,255 : 2d_pen_width 2
2d_line x0,y0,x0+x,y0-y : ' tracé d'un segment (vecteur)
2d_pen_color 0,0,0 : 2d_pen_width 1
2d_line x0+x,y0-y,x0+x,y0 : 2d_line x0+x,y0-y,x0,y0-y
print_locate x0+x+5,y0-y-6 : print "P"
print_locate x0+x-5,y0+5 : print "y"
print_locate x0-10,y0-y-6 : print "x"
' pause 1000
phi = 90 : ' angle de rotation
xprime = x * cos(phi) - y * sin(phi) : ' coordonnée x après rotation
yprime = y * cos(phi) + x * sin(phi) : ' coordonnée y après rotation
2d_pen_color 255,0,0 : 2d_pen_width 2
2d_line x0,y0,x0+xprime,y0-yprime
2d_pen_color 0,0,0 : 2d_pen_width 1
2d_line x0+xprime,y0-yprime,x0,y0-yprime : 2d_line x0+xprime,y0-yprime,x0+xprime,y0
print_locate x0+xprime,y0-yprime-15 : print "P'"
print_locate x0-12,y0-yprime-15 : print "x'"
print_locate x0+xprime,y0+5 : print "y'"
2d_pen_color 0,200,0 : 2d_pen_width 2
2d_arc x0,y0,20,110,22
print_locate x0+10,y0-30 : print "phi"
print_locate 10,300 : print "Le point P(x,y)"
print " a subi une rotation d'un angle phi dans"
print " le sens trigonométrique pour devenir "
print " le point P'(x',y')"
rem ============================================================================
| |
|   | | Marc

Nombre de messages : 2466
Age : 63
Localisation : TOURS (37)
Date d'inscription : 17/03/2014
 |  Sujet: Re: Rotation d'un point autour de l'origine Sujet: Re: Rotation d'un point autour de l'origine  Jeu 3 Mar 2022 - 20:48 Jeu 3 Mar 2022 - 20:48 | |
| - Papydall a écrit:
- Rotation d'un point autour de l'origine
Ton code-source est très pédagogique avec une très belle présentation graphique. Bravo et merci Papydall ! | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Rotation d'un point autour de l'origine Sujet: Re: Rotation d'un point autour de l'origine  Ven 4 Mar 2022 - 5:44 Ven 4 Mar 2022 - 5:44 | |
| | |
|   | | JL35
Nombre de messages : 7112
Localisation : 77
Date d'inscription : 29/11/2007
 |  Sujet: Re: Rotation d'un point autour de l'origine Sujet: Re: Rotation d'un point autour de l'origine  Ven 4 Mar 2022 - 16:40 Ven 4 Mar 2022 - 16:40 | |
| En fait papydall je voulais utiliser ton astuce pour faire la rotation d'une figure complète, (d'où mon intervention dans bavardages pour passer à une sub un tableau contenant les coordonnées des sommets et lui faire exécuter la rotation, et ta réponse). En attendant la sub ne fait que renvoyer les nouvelles coordonnées du point pivoté, il faut donc faire des appels successifs: - Code:
-
' Rotation d'une figure (ici rectangle) d'un angle donné
DIM w,h,xc,yc,xr(4),yr(4),x1(4),y1(4),i,phi,xa,ya
PICTURE 1: FULL_SPACE 1: 2D_TARGET_IS 1: 2D_FILL_OFF
DEGREES
xc = WIDTH(1)/2: yc = HEIGHT(1)/2: ' coordonnées du centre de rotation
2D_PEN_DOT: 2D_LINE xc,0,xc,HEIGHT(1): 2D_LINE 0,yc,WIDTH(1),yc: ' axes
2D_PEN_SOLID: 2D_PEN_WIDTH 2
w = 300: h = 200: ' dimensions du rectangle
' coordonnées des sommets du rectangle (centré)
xr(1) = xc-w/2: xr(2) = xc+w/2: xr(3) = xr(2): xr(4) = xr(1)
yr(1) = yc-h/2: yr(2) = yr(1): yr(3) = yc+h/2: yr(4) = yr(3)
2D_RECTANGLE xr(1),yr(1),xr(3),yr(3)
phi = 40: ' angle de rotation (sens des aiguilles, 0 à 360°) autour du centre
FOR i = 1 TO 4
Rotate(xr(i),yr(i),xc,yc,phi)
x1(i) = xa: y1(i) = ya
NEXT i
2D_PEN_COLOR 0,0,255
2D_LINE x1(1),y1(1),x1(2),y1(2): 2D_POLY_TO x1(3),y1(3)
2D_POLY_TO x1(4),y1(4): 2D_POLY_TO x1(1),y1(1)
END
' =============================================================================
SUB Rotate(x,y,x0,y0,phi)
' rotation du point x,y autour du point x0,y0 d'un angle phi degrés (papydall)
' résultat dans xa,ya (définis dans l'appelant)
x=x-x0: y=y0-y: ' par rapport au centre
xa=x*COS(phi)-y*SIN(phi) : ' coordonnée après rotation
ya=y*COS(phi)+x*SIN(phi) : ' (par rapport au centre de rotation)
xa = xa+x0: ya = ya+y0: ' coordonnées absolues
END_SUB
' ============================================================================= 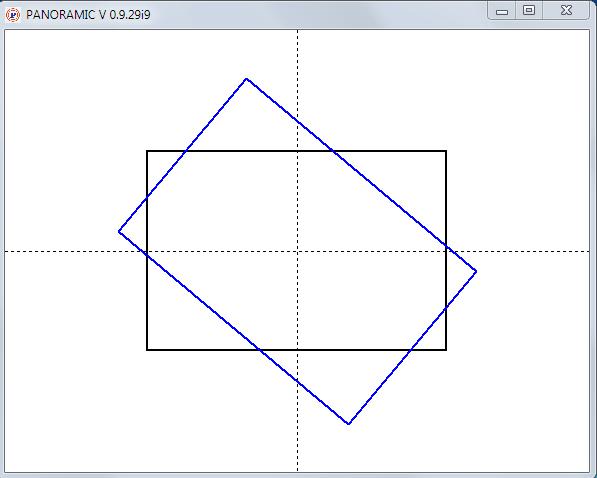 | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Rotation d'un point autour de l'origine Sujet: Re: Rotation d'un point autour de l'origine  Ven 4 Mar 2022 - 18:23 Ven 4 Mar 2022 - 18:23 | |
| @JL35 Revoies ce post - Code:
-
rem ============================================================================
' Rotation d'une figure autour de l'origine
' par Papydall
rem ============================================================================
dim x0,y0,a,newx,newy, zoom
picture 10 : full_space 10 : 2d_target_is 10
x0 = width(10)/2 : y0 = height(10)/2 : ' Coordonée de l'origine
zoom = 30 : ' facteur d'aggrandissement
Trace_Figure() : ' on trace une figure , une flèche vers le haut comme exemple
' On va tourner cette figure autour de l'origine
for a = 0 to 360 step 10 : ' Faire un tour complet
cls
2d_line 0,y0, 2*x0,y0 : ' tracé de l'axe horizontal
2d_line x0,0, x0,2*y0 : ' tracé de l'axe vertcal
Rotation_Figure(a) : ' Tourner la figure
pause 50
next a
end
rem ============================================================================
' Tracé d'une flèche comme exemple
SUB Trace_Figure()
dim_local i,p,x,y
restore
read p : read x : read y : 2d_poly_from x0 + zoom * x, y0 - zoom * y
for i = 2 to p
read x : read y : 2d_poly_to x0 + zoom * x,y0 - zoom * y
next i
END_SUB
rem ============================================================================
' Rotation de la flèche de l'exemple autour de l'origine des axes d'un angle en degrés
' Pour faire tourner une figure, il suffit de faire tourner tous ses points
SUB Rotation_Figure(angle)
dim_local i,p,x,y
restore
read p : read x : read y : Rotation_Point(x,y,angle)
2d_poly_from x0 + zoom * newx, y0 - zoom * newy
for i = 2 to p
read x : read y : Rotation_Point(x,y,angle)
2d_poly_to x0 + zoom * newx,y0 - zoom * newy
next i
END_SUB
rem ============================================================================
' Rotation autour de l'origine d'un point (x,y) d'un angle tetha en degrés.
' Pour effectuer une rotation à un point il suffit de multiplier ses coordonnées
' par la matrice de rotation suivante :
' cos(tetha) -sin(tetha)
' sin(tetha) cos(tetha)
SUB Rotation_Point(x,y,tetha)
degrees
newx = x * cos(tetha) - y * sin(tetha)
newy = x * sin(tetha) + y * cos(tetha)
END_SUB
rem ============================================================================
' dessin d'une flèche
data 8 : ' nombre de points de la figure
data 3,0 : ' coordonnées 1er point
data 4,0 : ' coordonnées 2ème point
data 4,3
data 5,3
data 3.5,4.5
data 2,3
data 3,3
data 3,0 : ' coordonnées dernier point qui est le même que le 1er pour boucler la boucle
rem ============================================================================
| |
|   | | JL35
Nombre de messages : 7112
Localisation : 77
Date d'inscription : 29/11/2007
 |  Sujet: Re: Rotation d'un point autour de l'origine Sujet: Re: Rotation d'un point autour de l'origine  Ven 4 Mar 2022 - 18:43 Ven 4 Mar 2022 - 18:43 | |
| Là tu m'as eu papydall, j'aurais mieux fait de faire une petite recherche avant de ramener ma fraise !  Et j'étais même intervenu à l'époque. Mais bon, ça date de 2014, le temps passe... Enfin, merci quand même ! | |
|   | | mindstorm

Nombre de messages : 685
Age : 55
Localisation : charente
Date d'inscription : 13/02/2013
 |  Sujet: Re: Rotation d'un point autour de l'origine Sujet: Re: Rotation d'un point autour de l'origine  Lun 7 Mar 2022 - 18:29 Lun 7 Mar 2022 - 18:29 | |
| Bonjour à tous Encore Bravo papydall pour tes post Une question qui nous permettrai d'approfondir le sujet. Je souhaite, par curiosité, connaitre la relation entre une rotation suivant l'axe X et la déformation de l'objet plan (rectangle) https://panoramic.1fr1.net/t4071-correction-de-parallaxe-de-vos-photo?highlight=parallaxeil serai tellement intéressant de connaitre l'angle de prise de vue d'une photo en mesurant les déformation de cette objet. Rien ne presse mon programme est de 2015 | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Rotation d'un point autour de l'origine Sujet: Re: Rotation d'un point autour de l'origine  Lun 7 Mar 2022 - 23:32 Lun 7 Mar 2022 - 23:32 | |
| Rappel 1 - Code:
-
rem ============================================================================
rem Les mathématiques pour
rem les transformations du plan
rem ============================================================================
rem Les principales transformations du plan sont :
rem * les translations,
rem * les changements d’échelles,
rem * les symétries,
rem * les rotations,
rem * les cisaillements.
rem ============================================================================
rem Le calcul matriciel résout tous ces problèmes.
rem Soient (x,y) les coordonnées d’un point du plan cartésien.
rem On peut considérer ces coordonnées comme une matrice de 1 ligne sur 2 colonnes
rem que nous noterons matrice (1 X 2) (lire matrice 1 croix 2).
rem ============================================================================
rem La matrice générale :
rem
rem A B
rem C D
rem
rem est une matrice de 2 lignes sur 2 colonnes et sera notée matrice (2 X 2)
rem (lire matrice 2 croix 2)
rem ============================================================================
rem Le produit matriciel de la matrice (1 X 2) et de la matrice (2 X 2) donne comme
rem résultat (A*x+C*y B*x+D*y)
rem
rem Donc, tout point du plan (x,y) multiplié par la matrice (2 X 2) a pour transformé
rem un nouveau point du plan (xp,yp) tel que :
rem ____________________
rem | |
rem | xp = A*x + C*y |
rem | yp = B*x + D*y |
rem |____________________|
rem
rem La transformation obtenue dépendra des valeurs données aux variables A,B,C,D.
rem ============================================================================
rem Pour information:
rem *****************
rem Voici les différentes matrices de transformations:
rem ----------------------------------------------------------------------------
rem Les changements d’échelles sont contrôlés par la matrice :
rem
rem A 0
rem 0 D
rem
rem En effet le produit matriciel donne A*x D*y d’où xp = A*x ; yp = D*y
rem ----------------------------------------------------------------------------
rem Les symétries : les matrices qui contrôlent les symétries ne sont que des cas
rem particuliers de la matrice changement d’échelles dans laquelle A et/ou D sont
rem négatifs.
rem
rem La matrice:
rem
rem -1 0
rem 0 1
rem
rem produira une symétrie par rapport à l’axe des Y
rem En effet le produit matriciel donne xp = -x ; yp = y
rem
rem La matrice:
rem
rem 1 0
rem 0 -1
rem
rem produira une symétrie par rapport à l’axe des X
rem En effet, le produit matriciel donne xp = x ; yp = -y
rem
rem La matrice:
rem
rem -1 0
rem 0 -1
rem
rem produira une symétrie par rapport aux deux axes c.à.d une symétrie
rem centrale par rapport à l’origine.
rem En effet, le produit matriciel donne xp = -x ; yp = -y
rem ----------------------------------------------------------------------------
rem Les cisaillements : les matrices qui contrôlent les cisaillements sont
rem
rem 1 0
rem C 1
rem
rem donnera un cisaillement en x
rem
rem 1 B
rem 0 1
rem
rem donnera un cisaillement en y
rem
rem 1 B
rem C 1
rem
rem donnera un cisaillement dans les deux directions
rem ----------------------------------------------------------------------------
rem Les rotations : Les matrices qui contrôlent les rotations sont :
rem
rem cos(theta) sin(theta)
rem -sin(theta) cos(theta)
rem
rem Les coefficients A,B,C,D de la matrice générale sont dans ce cas :
rem A = cos(theta) ; B = sin(theta) ; C = -sin(theta) ; D = cos(theta)
rem Avec theta l’angle de rotation du point autour de l’origine des axes.
rem Cet angle est exprimé en RADIANS.
rem ============================================================================
rem &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
rem ============================================================================
rem
rem Application : rotation d’un polygone
dim n : n = 4 : ' Nombre des sommets du polygone, ici c'est un carré
dim x(n+1),y(n+1)
dim A,B,C,D : ' termes de la matrice rotation
dim xc,yc : ' coordonnées du centre de l'écran
dim theta : ' angle de rotation
dim p : ' pas de variation de l'angle de rotation
caption 0 ,"Rotation d'un polygone autour de l'origine des axes"
picture 10 : full_space 10 : 2d_target_is 10
p = pi/18 : ' essayez avec p = pi/72 ou p = pi/36 ou p = pi/9 ou p = pi/144
xc = width_client(10)/2 : ' coordonnées du centre de l'écran et ...
yc = height_client(10)/2 : ' ... aussi centre de rotation
Init_polygone() : ' Mémorisation des somments du polygone
Trace_axes() : ' Tracé des axes
' Faire tourner le polygone autour du centre de rotation par un pas de p radians
for theta = 0 to 2*pi step p
Rotation(theta) : ' Faire tourner le polygone
pause 200 : ' pour suivre la rotation, valeur à modifier ou supprimer
next theta
end
rem ============================================================================
rem &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
rem ============================================================================
' Coordonnées relatives par rapport au centre de l'écran des sommets du polygone
' (ici un carré de 150 pixels de côté)
DATA 0,0 : ' 1er point
DATA 150,0 : ' 2ème point
DATA 150,150 : ' 3ème point
DATA 0,150 : ' 4ème point
rem ============================================================================
' Retourne les coefficients de la matrice(2 X 2) de rotation autour de l'origine
SUB Matrice_Rotation(theta)
A = cos(theta) : B = sin(theta) : C = 0-sin(theta) : D = cos(theta)
END_SUB
rem ============================================================================
' Mémorisation des somments du polygone
SUB Init_Polygone()
dim_local i
for i = 1 to n :read x(i):read y(i): next i
x(n+1) = x(1) : y(n+1) = y(1) : ' Pour fermer le polygone
END_SUB
rem ============================================================================
' Tracer des axes
SUB Trace_Axes()
2d_line 0,yc,2*xc,yc : ' tracer l'axe des X
2d_line xc,0,xc,2*yc : ' tracer l'axe des Y
END_SUB
rem ============================================================================
' Effectuer une rotation du polygone d'un angle theta en RADIANS
' puis tracer le nouveau polygone
SUB Rotation(theta)
Dim_local xp,yp,i
Matrice_Rotation(theta) : ' Calcul des coefficients de la matrice de rotation
xp = A * x(1) + C * y(1) : ' Calcul des nouvelles coordonnées du 1er point ...
yp = B * x(1) + D * y(1) : ' ... après avoir subi la rotation
2d_poly_from xc+xp,yc+yp : ' Tracé du point de départ du polygone
for i = 2 to n + 1
xp = A * x(i) + C * y(i) : ' Calcul des nouvelles coordonnées du point ...
yp = B * x(i) + D * y(i) : ' ... suivant après avoir subi la rotation
2d_poly_to xc+xp,yc-yp : ' Relier au point suivant
next i
END_SUB
rem ============================================================================
rem &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
rem ============================================================================
Rappel 2 - Code:
-
rem ============================================================================
rem Transformation conforme
rem Par Papydall
rem Utilisant la bibliothèque de calculs sur les nombres complexes de Jean_Debord
rem ============================================================================
Init()
Variables_Globales()
Transformation()
end
rem ============================================================================
SUB Init()
dim xi,xm,yi,ym,xmin,xmax,ymin,ymax,dx,dy,lx,ly
full_space 0 : color 0,0,0,0 : 2d_pen_color 0,255,255
dx = 51 : dy = 31 : lx = screen_x : ly = screen_y
xi = -1.55 : xm = 1.55 : yi = -1.55 : ym = 1.55
xmin = -5 : xmax = 5 : ymin = -3 : ymax = 3
dim reseauX(dx),reseauY(dy)
END_SUB
rem ============================================================================
SUB Plot(re1,im1,re2,im2)
dim_local x1,y1,x2,y2
x1 = int(lx*(re1-xmin)/(xmax-xmin))
y1 = int(ly*(im1-ymin)/(ymax-ymin))
x2 = int(lx*(re2-xmin)/(xmax-xmin))
y2 = int(ly*(im2-ymin)/(ymax-ymin))
2d_line x1,y1,x2,y2
END_SUB
rem ============================================================================
SUB Transformation()
dim_local i,j,re,im ,r1,i1
for i = 0 to dx
for j = 0 to dy
re = xi + i *(xm-xi)/dx
im = yi + j *(ym-yi)/dy
' Essayez une à une ces différentes fonctions
CInv(re,im) : ' f(z) = 1/z
' CTan(re,im) : ' f(z) = tan(z)
' CCos(re,im) : ' f(z) = cos(z)
' CSin(re,im) : ' f(z) = sin(z)
' CSquare(re,im): ' f(z) = z*z
' CCube(re,im) : ' f(z) = z*z*z
' CSqrt(re,im) : ' f(z) = sqr(z)
' CLog(re,im) : ' f(z) = Log(z)
' CExp(re,im) : ' f(z) = Exp(z)
' CRealPower(re,im,5.3) : ' f(z) = z^p avec p réel = 5.3 dans ce cas
' CPower(re,im,3/2,-1) : ' f'z) = z^c avec c complexe = 1.5 - i dans ce cas
' CSinh(re,im) : ' f(z) = hsin(z)
' CCosh(re,im) : ' f(z) = hcos(z)
' CTanh(re,im) : ' f(z) = htan(z)
' CASin(re,im) : ' f(z) = ArcSin(z)
' CACos(re,im) : ' f(z) = ArcCos(z)
' CATan(re,im) : ' f(z) = ArcTan(z)
' CASinh(re,im) : ' f(z) = ArcHSin(z)
' CACosh(re,im) : ' f(z) = ArcHcos(z)
' CATanh(re,im) : ' f(z) = ARCHTan(z)
if j > 0 then plot(reseauX(j-1),reseauY(j-1),r_x,r_y)
if i > 0 then plot(reseauX(j),reseauY(j),r_x,r_y)
reseauX(j) = r_x : reseauY(j) = r_y
next j
next i
END_SUB
rem ============================================================================
rem Bibliothèque de calculs sur les nombres complexes
rem Par Jean Debord
rem ============================================================================
rem ============================================================================
SUB Variables_Globales()
' Constantes mathematiques
dim MaxNum, MinNum, MaxLog, MinLog, PiDiv2
MaxLog = 709.78 : ' Argument max. pour EXP
MinLog = -708.39 : ' Argument min. pour EXP
MaxNum = exp(MaxLog) : ' Nb reel max. ~ 2^1024
MinNum = exp(MinLog) : ' Nb reel min. ~ 2^(-1022)
PiDiv2 = Pi / 2
' Resultats des calculs
' Partie reelle, partie imaginaire, module, argument, signe
dim r_x, r_y, r_mod, r_arg, r_sgn
' Code d'erreur
' 0 = pas d'erreur
' -1 = argument hors bornes
' -2 = singularite
' -3 = overflow
' -4 = underflow
dim ErrCode%
END_SUB
rem ============================================================================
sub CMul(a_x, a_y, b_x, b_y)
' Multiplication : r_x + i r_y = (a_x + i a_y) * (b_x + i b_y)
ErrCode% = 0
r_x = a_x * b_x - a_y * b_y
r_y = a_x * b_y + a_y * b_x
end_sub
rem ============================================================================
sub CSquare(a_x, a_y)
' Carre : r_x + i r_y = (a_x + i a_y)^2
ErrCode% = 0
r_x = a_x * a_x - a_y * a_y
r_y = 2 * a_x * a_y
end_sub
rem ============================================================================
sub CCube(a_x, a_y)
' Cube : r_x + i r_y = (a_x + i a_y)^3
dim_local x2, y2, x3, y3
ErrCode% = 0
x2 = a_x * a_x : x3 = x2 * a_x
y2 = a_y * a_y : y3 = y2 * a_y
r_x = x3 - 3 * a_x * y2
r_y = 3 * x2 * a_y - y3
end_sub
rem ============================================================================
sub CIntPower(a_x, a_y, n%)
' Puissance entiere : r_x + i r_y = (a_x + i a_y)^n
dim_local m%, b_x, b_y, res_x, res_y
ErrCode% = 0
if a_x = 0 and a_y = 0
if n% = 0
' 0^0 = lim x^x quand x --> 0 = 1
r_x = 1
r_y = 0
else
if n% > 0
' 0^n = 0 si n > 0
r_x = 0
r_y = 0
else
' 0^n indefini si n < 0
ErrCode% = -2
r_x = MaxNum
r_y = MaxNum
end_if
end_if
else
if n% < 0
m% = abs(n%)
CInv(a_x, a_y)
b_x = r_x
b_y = r_y
else
m% = n%
b_x = a_x
b_y = a_y
end_if
res_x = 1 : res_y = 0
while m% > 0
if odd(m%) = 1
CMul(b_x, b_y, res_x, res_y)
res_x = r_x
res_y = r_y
end_if
CSquare(b_x, b_y)
b_x = r_x
b_y = r_y
m% = int(m% / 2)
end_while
r_x = res_x
r_y = res_y
end_if
end_sub
rem ============================================================================
sub CDiv(a_x, a_y, b_x, b_y)
' Division : r_x + i r_y = (a_x + i a_y) / (b_x + i b_y)
' Algorithme d'apres "Numerical Recipes"
dim_local q, t
if b_x = 0 and b_y = 0
ErrCode% = -3
r_x = MaxNum
r_y = MaxNum
else
ErrCode% = 0
if abs(b_x) >= abs(b_y)
q = b_y / b_x
t = b_x + b_y * q
r_x = (a_x + a_y * q) / t
r_y = (a_y - a_x * q) / t
else
q = b_x / b_y
t = b_x * q + b_y
r_x = (a_x * q + a_y) / t
r_y = (a_y * q - a_x) / t
end_if
end_if
end_sub
rem ============================================================================
sub CInv(a_x, a_y)
' Inverse : r_x + i r_y = 1 / (a_x + i a_y)
dim_local Temp
if a_x = 0 and a_y = 0
ErrCode% = -3
r_x = MaxNum
r_y = MaxNum
else
ErrCode% = 0
Temp = a_x * a_x + a_y * a_y
r_x = a_x / Temp
r_y = 0 - a_y / Temp
end_if
end_sub
rem ============================================================================
sub CSgn(a_x, a_y)
' Signe complexe
ErrCode% = 0
if a_x > 0
r_sgn = 1
else
if a_y < 0
r_sgn = -1
else
if a_y > 0
r_sgn = 1
else
if a_y < 0
r_sgn= -1
else
r_sgn = 0
end_if
end_if
end_if
end_if
end_sub
rem ============================================================================
sub CAbs(a_x, a_y)
' Module : r_mod = |a_x + i a_y|
' Algorithme d'apres "Numerical Recipes"
ErrCode% = 0
dim_local AbsX, AbsY, R, C
AbsX = abs(a_x)
AbsY = abs(a_y)
if a_x = 0
r_mod = abs(a_y)
else
if a_y = 0
r_mod = abs(a_x)
else
if AbsX > AbsY
R = AbsY / AbsX
C = AbsX
else
R = AbsX / AbsY
C = AbsY
end_if
r_mod = C * sqr(1 + R * R)
end_if
end_if
end_sub
rem ============================================================================
sub CArg(a_x, a_y)
' Argument : r_arg = arg(a_x + i a_y)
' Resultat dans [-Pi, Pi)
' Equivaut a atan2(a_y, a_x)
ErrCode% = 0
if a_x = 0
r_arg = sgn(a_y) * PiDiv2
else
' 4e / 1er quadrant : -Pi/2..Pi/2
r_arg = atn(a_y / a_x)
if a_x < 0
if a_y > 0
' 2e quadrant : Pi/2..Pi
r_arg = r_arg + Pi
else
' 3e quadrant : -Pi..-Pi/2
r_arg = r_arg - Pi
end_if
end_if
end_if
end_sub
rem ============================================================================
sub ATan2(y, x)
' atn(y/x) --> Resultat dans [-Pi, Pi)
CArg(x, y)
end_sub
rem ============================================================================
sub CSqrt(a_x, a_y)
' Racine carree : r_x + i r_y = sqrt(a_x + i a_y)
' Algorithme d'apres "Numerical Recipes"
dim_local X, Y, W, R
X = abs(a_x)
Y = abs(a_y)
ErrCode% = 0
if a_x = 0 and a_y = 0
r_x = 0
r_y = 0
else
if X >= Y
R = Y / X
W = sqr(X) * sqr(0.5 * (1 + sqr(1 + R * R)))
else
R = X / Y
W = sqr(Y) * sqr(0.5 * (R + sqr(1 + R * R)))
end_if
if a_x >= 0.0
r_x = W
r_y = a_y / (2 * r_x)
else
if a_y >= 0
r_y = W
else
r_y = 0 - W
end_if
r_x = a_y / (2 * r_y)
end_if
end_if
end_sub
rem ============================================================================
sub CLog(a_x, a_y)
' Partie principale du logarithme complexe
' r_x + i r_y = ln(a_x + i a_y)
if a_x = 0 and a_y = 0
ErrCode% = -2
r_x = 0 - MaxNum
r_y = 0
else
ErrCode% = 0
CAbs(a_x, a_y)
CArg(a_x, a_y)
r_x = log(r_mod)
r_y = r_arg
end_if
end_sub
rem ============================================================================
sub CExp(a_x, a_y)
' Exponentielle complexe : r_x + i r_y = exp(a_x + i a_y)
dim_local ExpX
if a_x < MinLog
ErrCode% = -4
r_x = 0
r_y = 0
else
if a_x > MaxLog
ErrCode = -3
ExpX = MaxNum
else
ErrCode% = 0
ExpX = exp(a_x)
end_if
r_x = ExpX * cos(a_y)
r_y = ExpX * sin(a_y)
end_if
end_sub
rem ============================================================================
sub CRealPower(a_x, a_y, p)
' Puissance (exposant reel) : (a_x + i a_y)^p
' Resultat dans r_x, r_y
' Resultat aussi dans r_mod, r_arg si a <> 0
ErrCode% = 0
if a_x = 0 and a_y = 0
if p = 0
' 0^0 = lim x^x quand x --> 0 = 1
r_x = 1
r_y = 0
else
if p > 0
' 0^p = 0 si p > 0
r_x = 0
r_y = 0
else
' 0^p indefini si p < 0
ErrCode% = -2
r_x = MaxNum
r_y = MaxNum
end_if
end_if
else
CAbs(a_x, a_y)
CArg(a_x, a_y)
r_mod = power(r_mod, p)
r_arg = r_arg * p
r_x = r_mod * cos(r_arg)
r_y = r_mod * sin(r_arg)
end_if
end_sub
rem ============================================================================
sub CPower(a_x, a_y, b_x, b_y)
' Puissance (exposant complexe) : (a_x + i a_y)^(b_x + i b_y)
' Resultat dans r_x, r_y
ErrCode% = 0
if a_x = 0 and a_y = 0
if b_x = 0 and b_y = 0
' 0^0 = lim x^x quand x --> 0 = 1
r_x = 1
r_y = 0
else
' 0^p = 0 si p > 0
r_x = 0
r_y = 0
end_if
else
' exp(b ln(a))
CAbs(a_x, a_y)
CArg(a_x, a_y)
CMul(b_x, b_y, log(r_mod), r_arg)
CExp(r_x, r_y)
end_if
end_sub
rem ============================================================================
sub CSin(a_x, a_y)
' Sinus complexe : r_x + i r_y = sin(a_x + i a_y)
ErrCode% = 0
r_x = sin(a_x) * hcos(a_y)
r_y = cos(a_x) * hsin(a_y)
end_sub
rem ============================================================================
sub CCos(a_x, a_y)
' Cosinus complexe : r_x + i r_y = cos(a_x + i a_y)
ErrCode% = 0
r_x = cos(a_x) * hcos(a_y)
r_y = 0 - sin(a_x) * hsin(a_y)
end_sub
rem ============================================================================
sub CSinh(a_x, a_y)
' Sinus hyperbolique complexe : r_x + i r_y = sinh(a_x + i a_y)
ErrCode% = 0
r_x = hsin(a_x) * cos(a_y)
r_y = hcos(a_x) * sin(a_y)
end_sub
rem ============================================================================
sub CCosh(a_x, a_y)
' Cosinus hyperbolique complexe : r_x + i r_y = cosh(a_x + i a_y)
ErrCode% = 0
r_x = hcos(a_x) * cos(a_y)
r_y = hsin(a_x) * sin(a_y)
end_sub
rem ============================================================================
sub CTan(a_x, a_y)
' Tangente complexe : r_x + i r_y = tan(a_x + i a_y)
dim_local X2, Y2, Temp
X2 = 2 * a_x
Y2 = 2 * a_y
Temp = cos(X2) + hcos(Y2)
if Temp <> 0
ErrCode% = 0
r_x = sin(X2) / Temp
r_y = hsin(Y2) / Temp
else
' a = Pi/2 + k*Pi
ErrCode% = -2
r_x = MaxNum
r_y = 0
end_if
end_sub
rem ============================================================================
sub CTanh(a_x, a_y)
' Tangente hyperbolique complexe : r_x + i r_y = tanh(a_x + i a_y)
dim_local X2, Y2, Temp
X2 = 2.0 * a_x
Y2 = 2.0 * a_y
Temp = hcos(X2) + cos(Y2)
if Temp = 0
' a = i * (Pi/2 + k*Pi)
ErrCode% = -2
r_x = 0
r_y = MaxNum
else
ErrCode% = 0
r_x = hsin(X2) / Temp
r_y = sin(Y2) / Temp
end_if
end_sub
rem ============================================================================
sub CASin(a_x, a_y)
' Arc Sinus complexe : r_x + i r_y = asin(a_x + i a_y)
dim_local X2, XX, YY, Rp, Rm, S, T
X2 = 2 * a_x
XX = a_x * a_x
YY = a_y * a_y
S = XX + YY + 1
Rp = 0.5 * sqr(S + X2)
Rm = 0.5 * sqr(S - X2)
T = Rp + Rm
ErrCode% = 0
CSgn(a_y, 0 - a_x)
r_x = asin(Rp - Rm)
r_y = r_sgn * log(T + sqr(T * T - 1))
end_sub
rem ============================================================================
sub CACos(a_x, a_y)
' Arc Cosinus complexe :
' r_x + i r_y = acos(a_x + i a_y) = Pi/2 - ASin(a)
CASin(a_x, a_y)
r_x = PiDiv2 - r_x
r_y = 0 - r_y
end_sub
rem ============================================================================
sub CATan(a_x, a_y)
' Arc Tangente complexe : r_x + i r_y = atan(a_x + i a_y)
dim_local XX, YY, Yp1, Ym1, A1, A2
if a_x = 0 and abs(a_y) = 1
' a = +/- i
ErrCode% = -2
r_x = 0
r_y = sgn(a_y) * MaxNum
else
ErrCode% = 0
XX = a_x * a_x
YY = a_y * a_y
Yp1 = a_y + 1
Ym1 = a_y - 1
CArg(0 - Ym1, a_x) : A1 = r_arg : ' = atan2(a_x, - Ym1)
CArg(Yp1, 0 - a_x) : A2 = r_arg : ' = atan2(- Ym1, a_x)
r_x = 0.5 * (A1 - A2)
r_y = 0.25 * log((XX + Yp1 * Yp1) / (XX + Ym1 * Ym1))
end_if
end_sub
rem ============================================================================
sub CASinh(a_x, a_y)
' Argument Sinus hyperbolique complexe :
' r_x + i r_y = asinh(a_x + i a_y) = -i*asin(i*a)
' i * (a_x + i a_y) = -a_y + i a_x
dim_local t
CASin(0 - a_y, a_x)
t = r_x
r_x = r_y
r_y = 0 - t
end_sub
rem ============================================================================
sub CACosh(a_x, a_y)
' Argument Cosinus hyperbolique complexe :
' r_x + i r_y = acosh(a_x + i a_y) = csgn(a_y + i(1 - a_x)) * i * acos(a)
dim_local t
CSgn(a_y, 1 - a_x)
CACos(a_x, a_y)
t = r_x
r_x = 0 - r_sgn* r_y
r_y = r_sgn * t
end_sub
rem ============================================================================
sub CATanh(a_x, a_y)
' Argument Tangente hyperbolique complexe :
' r_x + i r_y = atanh(a_x + i a_y) = -i*atan(i*a)
dim_local t
CATan(0 - a_y, a_x)
t = r_x
r_x = r_y
r_y = 0 - t
end_sub
rem ============================================================================
- Code:
-
rem ============================================================================
rem Transformations affines
rem par Papydall
rem ============================================================================
rem Les transformations suivantes sont données avec leurs matrices de transformation
rem Etirement (changement d’échelle) selon les axes
rem Rotation autour de l’origine
rem Inclinaison le long de l’axe des X
rem Inclinaison le long de l’axe des Y
rem Déplacement relatif par rapport aux axes X et/ou Y
rem ============================================================================
Init()
Trace_Figure() : ' Tracer la flèche comme figure exemple
input bidon$ : cls
Etirement_Figure(1/4,1) : ' changement d'échelle (1/4 donc rapetissement) selon l'axe X, inchangé selon l'axe Y (1)
Etirement_Figure(2,1) : ' changement d'échelle (2 donc agrandissement) selon l'axe X, inchangé selon l'axe Y (1)
Etirement_Figure(4,1/3) : ' Agrandissement 4 fois selon l'axe X et rapetissement 1/3 selon l'axe Y
caption 20,"Changement d'échelle selon les axes X et Y"
caption 20,caption$(20) + chr$(13) + string$(30," ") + "<Entree> pour la suite" : input bidon$ : cls
Rotation() : ' Rotation autour de l'origines des axes
caption 20, "<Entree> pour la suite"
Inclinaison_Figure("x",45) : ' Inclinaisons de 45° le long de de l'axe X
caption 20,"Inclinaison le long de l'axe des X de 45°"
caption 20,caption$(20) + chr$(13) + string$(20," ") + "<Entree> pour la suite" : input bidon$ : cls
Inclinaison_Figure("y",60) : ' Inclinaisons de 60° le long de de l'axe Y
caption 20,"Inclinaison le long de l'axe des Y de 60°"
caption 20,caption$(20) + chr$(13) + string$(20," ") + "<Entree> pour la suite" : input bidon$ : cls
Translation_Figure(-3,0) : ' Déplacement relatif par rapport à l'axe X
Translation_Figure(-5,6) : ' déplacement relatif par rapport aux deux axes X et Y
Translation_Figure(-9,-5): ' déplacement relatif par rapport aux deux axes X et Y
caption 20,"Translation de la figure <Entree> pour la suite" : input bidon$ : cls
caption 20,"That's all Folks !" + chr$(13) + "<Entree> pour terminer"
input bidon$
for a = 2*y0 to 10 step -10 : height 0,a : pause 50 : next a
terminate
end
rem ============================================================================
SUB Init()
dim x0,y0,a,newx,newy,zoom,bidon$
full_space 0
picture 10 : full_space 10 : 2d_target_is 10 : print_target_is 10
font_bold 10 : font_color 10,0,0,255
font_size 10,12
x0 = width(10)/2 : y0 = height(10)/2 : ' Coordonée de l'origine
zoom = 30 : ' facteur d'aggrandissement
alpha 20 : top 20,50 : left 20,100 : font_bold 20 : font_name 20,"tahoma"
font_color 20 ,100,50,20 : font_size 20, 14 : color 20,255,255,255
caption 20,"C'est sur cette flèche que nous allons tester les transformations affines :"
caption 20,caption$(20) + chr$(13) + "Changement d'échelle selon les axes,"
caption 20,caption$(20) + chr$(13) + "Rotation autour de l'origine,"
caption 20,caption$(20) + chr$(13) + "Inclinaison le long des axes,"
caption 20,caption$(20) + chr$(13) + "Déplacement relatif par rapport aux axes X et/ou Y."
caption 20,caption$(20) + chr$(13) + string$(30," ") + "<Entree> pour commencer"
degrees : ' on travaille en degrés
END_SUB
rem ============================================================================
' Tracé d'une flèche comme exemple
SUB Trace_Figure()
dim_local i,p,x,y
restore
read p : read x : read y : 2d_poly_from x0 + zoom * x, y0 - zoom * y
for i = 2 to p
read x : read y : 2d_poly_to x0 + zoom * x,y0 - zoom * y
next i
2d_pen_color 255,0,0 : 2d_fill_color 255,0,0 : 2d_circle x0,y0,5
2d_line x0-50,y0, x0+50,y0 : ' tracé de l'axe horizontal
2d_line x0,y0-50, x0,y0+50 : ' tracé de l'axe vertical
2d_pen_color 0,0,0
read x : read y : 2d_flood x0 + zoom * x,y0 - zoom * y , 0,0,0
2d_fill_color 255,255,255
print_locate x0 + zoom * (x+2),y0 - zoom * (y-1) : print "Figure exemple"
END_SUB
rem ============================================================================
SUB Rotation()
caption 20,"Rotation autour de l'origine ..."
Trace_Figure() : ' on trace une figure , une flèche vers le haut comme exemple
' On va faire tourner cette figure autour de l'origine
for a = 0 to 2*360 step 10 : ' Faire un tour complet
cls : 2d_pen_color 255,0,0 : 2d_fill_color 255,0,0 : 2d_circle x0,y0,5
2d_line x0-50,y0, x0+50,y0 : ' tracé de l'axe horizontal
2d_line x0,y0-50, x0,y0+50 : ' tracé de l'axe vertical
2d_pen_color 0,0,0
Rotation_Figure(a) : ' Faire tourner la figure
pause 100
next a
END_SUB
rem ============================================================================
' Rotation de la flèche de l'exemple autour de l'origine des axes d'un angle en dégrés
' Pour faire tourner une figure, il suffit de faire tourner tous ses points
SUB Rotation_Figure(angle)
dim_local i,p,x,y
restore
read p : read x : read y : Rotation_Point(x,y,angle)
2d_poly_from x0 + zoom * newx, y0 - zoom * newy
for i = 2 to p
read x : read y : Rotation_Point(x,y,angle)
2d_poly_to x0 + zoom * newx,y0 - zoom * newy
next i
read x : read y : Rotation_Point(x,y,angle)
2d_flood x0 + zoom * newx,y0 - zoom * newy , 0,0,0
2d_fill_color 255,255,255
print_locate x0 + zoom * (x+5),y0 - zoom * (y-1)
print "Rotation de la figure autour de l'origine"
END_SUB
rem ============================================================================
' Rotation autour de l'origine d'un point (x,y) d'un angle tetha en degrés.
' Pour effectuer une rotation à un point il suffit de multiplier ses coordonnées
' par la matrice de rotation suivante :
' cos(tetha) -sin(tetha)
' sin(tetha) cos(tetha)
SUB Rotation_Point(x,y,tetha)
newx = x * cos(tetha) - y * sin(tetha)
newy = x * sin(tetha) + y * cos(tetha)
END_SUB
rem ============================================================================
' Inclinaison de la flèche de l'exemple le long de l'axe des X ou l'axe des Y
' d'un angle a en degrés
' paramètre : axe$ = "X" <---- inclinaison le long de l'axe des X
' paramètre : axe$ = "Y" <---- inclinaison le long de l'axe des Y
SUB Inclinaison_Figure(axe$,a)
dim_local i,p,x,y
if upper$(axe$) <> "X" and upper$(axe$) <> "Y"
message "ERREUR !" + chr$(13) + "Vous avez indiqué un mauvais axe !"
exit_sub
end_if
cls
restore
read p : read x : read y : Inclinaison_Point(x,y,axe$,a)
2d_poly_from x0 + zoom * newx, y0 - zoom * newy
for i = 2 to p
read x : read y : Inclinaison_Point(x,y,axe$,a)
2d_poly_to x0 + zoom * newx,y0 - zoom * newy
next i
2d_pen_color 255,0,0 : 2d_fill_color 255,0,0 : 2d_circle x0,y0,5
2d_line x0-50,y0, x0+50,y0 : ' tracé de l'axe horizontal
2d_line x0,y0-50, x0,y0+50 : ' tracé de l'axe vertical
2d_pen_color 0,0,0
read x : read y : Inclinaison_Point(x,y,axe$,a)
2d_flood x0 + zoom * newx,y0 - zoom * newy , 0,0,0
2d_fill_color 255,255,255
if upper$(axe$) = "X"
print_locate x0 + zoom * (x+5),y0 - zoom * (y-1)
else
print_locate x0 + zoom * (x+3),y0 - zoom * (y+5)
end_if
print "Inclinaison le long de l'axe " + upper$(axe$) + " d'un angle de " + str$(a) +"°"
END_SUB
rem ============================================================================
' Les matrices de l'inclinaison sont :
' le long de l'axe des X :
' 1 tan(a)
' 0 1
' Le long de l'axe des Y :
' 1 0
' tan(a) 1
SUB Inclinaison_Point(x,y,axe$,a)
if upper$(axe$) = "X"
newx = x * 1 + y * tan(a)
newy = x * 0 + y * 1
else
newx = x * 1 + y * 0
newy = x * tan(a) + y * 1
end_if
END_SUB
rem ============================================================================
' Etirement de la flèche de l'exemple selon les axes X / Y
' Pour étirer une figure, il suffit d'étirer tous ses points
SUB Etirement_Figure(sx,sy)
dim_local i,p,x,y
restore
read p : read x : read y : Etirer_Point(x,y,sx,sy)
2d_poly_from x0 + zoom * newx, y0 - zoom * newy
for i = 2 to p
read x : read y : Etirer_Point(x,y,sx,sy)
2d_poly_to x0 + zoom * newx,y0 - zoom * newy
next i
2d_pen_color 255,0,0 : 2d_fill_color 255,0,0 : 2d_circle x0,y0,5
2d_line x0-50,y0, x0+50,y0 : ' tracé de l'axe horizontal
2d_line x0,y0-50, x0,y0+50 : ' tracé de l'axe vertical
2d_pen_color 0,0,0
read x : read y : Etirer_Point(x,y,sx,sy)
2d_flood x0 + zoom * newx,y0 - zoom * newy , 0,0,0
2d_fill_color 255,255,255
print_locate x0 + zoom * (x+4),y0 - zoom * (y-4)
print "Etirement selon les axes X / Y"
END_SUB
rem ============================================================================
' Etirement d'un point (x,y) selon les axes d'un facteur sx et xy.
' Pour effectuer un étirement à un point il suffit de multiplier ses coordonnées
' par la matrice d'étirement suivante :
' sx 0
' 0 sy
SUB Etirer_Point(x,y,sx,sy)
newx = x * sx
newy = y * sy
END_SUB
rem ============================================================================
SUB Translation_Figure(tx,ty)
dim_local i,p,x,y,t$
restore
read p : read x : read y : Translater_Point(x,y,tx,ty)
2d_poly_from x0 + zoom * newx, y0 - zoom * newy
for i = 2 to p
read x : read y : Translater_Point(x,y,tx,ty)
2d_poly_to x0 + zoom * newx,y0 - zoom * newy
next i
2d_pen_color 255,0,0 : 2d_fill_color 255,0,0 : 2d_circle x0,y0,5
2d_line x0-50,y0, x0+50,y0 : ' tracé de l'axe horizontal
2d_line x0,y0-50, x0,y0+50 : ' tracé de l'axe vertical
2d_pen_color 0,0,0
read x : read y : Translater_Point(x,y,tx,ty)
2d_flood x0 + zoom * newx,y0 - zoom * newy , 0,0,0
2d_fill_color 255,255,255
print_locate x0 + zoom * (newx+2),y0 - zoom * (newy-1)
if tx <> 0 and ty <> 0
t$ = "aux axes X et Y"
else
if tx <> 0 and ty = 0
t$ = "à l'axe X"
else
t$ = "à l'axe Y"
end_if
end_if
print "Déplacement relatif par rapport " + t$
END_SUB
rem ============================================================================
SUB Translater_Point(x,y,tx,ty)
newx = x + tx
newy = y + ty
END_SUB
rem ============================================================================
' dessin d'une flèche
data 8 : ' nombre de points de la figure
data 3,0 : ' coordonnées 1er point
data 4,0 : ' coordonnées 2ème point
data 4,3
data 5,3
data 3.5,4.5
data 2,3
data 3,3
data 3,0 : ' coordonnées dernier point qui est le même que le 1er pour boucler la boucle
data 3.5,3 : ' coordonnées du flood
rem ============================================================================
| |
|   | | mindstorm

Nombre de messages : 685
Age : 55
Localisation : charente
Date d'inscription : 13/02/2013
 |  Sujet: Re: Rotation d'un point autour de l'origine Sujet: Re: Rotation d'un point autour de l'origine  Mar 8 Mar 2022 - 18:59 Mar 8 Mar 2022 - 18:59 | |
|  Merci papydall je vais tenter de digérer tout cela au calme. A la première lecture, tout est clair et détaillé et cela me rassure. A suivre Deuxième lecture "Transformation conforme" me laisse un espoir de réussite l'illustration est très parlante Merci papydall | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Rotation d'un point autour de l'origine Sujet: Re: Rotation d'un point autour de l'origine  | |
| |
|   | | | | Rotation d'un point autour de l'origine |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
