Calcul de PI à l'aide des formules de développement en série

Salut tout le monde.

A tous ceux qui n’ont plus beaucoup d’idées pour programmer.
A tous ceux qui suivent le forum sans se manifester.
A tous ceux qui hésitent à nous faire partager leurs codes sous prétexte qu’ils ne sont pas intéressants.
A tous ceux qui sont au confinement volontaire ou imposé (vous n’êtes pas obligés de confiner aussi vos codes ou simplement vos avis et vos commentaires)
A tous ceux qui seront intéressés pour relever le challenge
A Jack également pour nous exhiber sa façon de coder
Enfin, à toux ceux qui veulent réanimer le forum

Je vous propose le challenge suivant :
Calcul de PI par des formules basées sur un développement en série.

Ci-après un « squelette » de code dans lequel les formules des calculs sont données dans les lignes REM avant chaque FNC.
Il s’agit de compléter l’une (ou toutes) des FNC.
Ma contribution est le codage de la Formule basée sur les moyennes arithmétique et géométrique , celle de Salamin-Brent.

Etes-vous prêts à relever le challenge ?

Voici le code-squelette

Code:: rem ============================================================================
rem Calcul de PI par des formules basées sur un développement en série.
rem ============================================================================
rem Si vous accepter de relever le challenge,
rem Veuillez complétez le code de l’une ou des 7 FNC suivantes en mettant vos
rem pseudos en REM au debut
rem ============================================================================
dim quelqueChose

font_name 0,"fixedsys" : font_bold 0
' ...
' ...
' etc

print "PI = " + str$(Pi_Salamin_Brent()) + " <--- Formule Salamin-Brent"
print "PI = " + str$(pi) + " <--- Panoramic"

end
rem ============================================================================
' Formule de Leonhard Euler (1707-1783)
' PI² = 6 * (1 + 1/2² + 1/3² + 1/4² + 1/5² ......)
FNC Pi_Euler()
   ' ....
   ' ....
   ' ....
   result quelqueChose
END_FNC
rem ============================================================================
' Développement en série de arctg x avec x = 1
' (W.Leibniz 1646-1716 ou James Gregory 1638- 1675)
' pi = 4 * (1 - 1/3 + 1/5 - 1/7 + 1/9 ......)
FNC Pi_AtnX_1()
   ' ....
   ' ....
   ' ....
   result quelqueChose
END_FNC
rem ============================================================================
' Développement en série de arctg x avec x = sqr(3) / 3 (Euler)
' pi = 2 * sqr(3) * (1 - 1/3 * 1/3¹ + 1/5 * 1/3² - 1/7 * 1/3³ + ...)
FNC Pi_AtnX_SQR3()
   ' ...
   ' ...
   ' ...
   result quelqueChose
END_FNC
rem ============================================================================
' Formule de John Machin (1685-1751) à partir de arctg 1/5 - arctg 1/239
' pi = 16 * (1/5^1 - 1/3 * 1/5^3 + 1/5 * 1/5^5 - 1/7 * 5^7 + ...)
' - 4 * (1/239^1 - 1/3 * 1/239^3 + 1/5 * 1/239^5 - 1/7 * 1/239^7 + ...)
FNC Pi_Machin()
   ' ...
   ' ...
   ' ...
   result quelqueChose
END_FNC
rem ============================================================================
' Formule de John Wallis (1616-1703)
' pi = 2 * (2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * ...)
FNC Pi_Wallis()
   ' ...
   ' ...
   ' ...
   result quelqueChose
END_FNC
rem ============================================================================
' Formule de François Viète (1540-1603)
' 2/pi = sqr(1/2) * sqr(1/2 + 1/2 * sqr(1/2)) * ...
FNC Pi_Viete()
   ' ...
   ' ...
   ' ...
   result quelqueChose
END_FNC
rem ============================================================================
' Formule de Brouncker (1620-1684)
' 4/pi = 1+1²/(2+3²/(2+5²/(2+7²/.....)))
FNC Pi_Brouncker()
   ' ...
   ' ...
   ' ...
   result quelqueChose
END_FNC
rem ============================================================================
' Formule basée sur les moyennes arithmétique et géométrique.
' Formule découverte par Eugène Salamin et Richard Brent en 1976
' a0 = 1 : b0 = 1/sqr(2)
' a(n+1) = (a(n)+ b(n)) / 2 : b(n+1) = sqr(a(n) * b(n))
' Un = 4*a²(n) / (1 - 2 * somme(2^i * (a²(i) - b²(i)))) ; i de 1 = n
' n ---> infini ; Un ---> pi
' ------------------------------------------------------------------------------
' Papydall
FNC Pi_Salamin_Brent()
   dim_local s_carre, puissance2,a,b,an,bn,Un,u,epsilon
   epsilon = 1E-6
   s_carre = 0 : puissance2 = 1 : an = 1 : bn = 1/sqr(2)
   u = 1 : Un = 0
   while not(abs(u-un) < epsilon)
   a = an : b = bn : u = Un
   an = (a+b)/2 : bn = sqr(a*b)
   puissance2 = puissance2 * 2
   s_carre = s_carre + puissance2 * (an*an - bn*bn)
   Un = 4*an*an / (1-2*s_carre)
   end_while
   result Un
END_FNC
rem ============================================================================

REM : même si vous n'êtes pas prêts pour coder, vous pouvez toujours réagir, question de déclencher un échange d'idées et de rompre le silence qui règne sur le forum.
Et si personne ne se manifestera pas, je compléterais moi-même mon code Crying or Very sad

Bonjour à tous !

John Wallis pour moi : certes imprécis mais simple pour un dimanche lol!

Code:

Code:: rem ============================================================================
rem Calcul de PI par des formules basées sur un développement en série.
rem ============================================================================
rem Si vous accepter de relever le challenge,
rem Veuillez complétez le code de l’une ou des 7 FNC suivantes en mettant vos
rem pseudos en REM au debut
rem ============================================================================
dim quelqueChose

font_name 0,"fixedsys" : font_bold 0
' ...
' ...
' etc
print "PI = " + str$(Pi_Wallis()) + " <--- Formule John Wallis"
print "PI = " + str$(Pi_Salamin_Brent()) + " <--- Formule Salamin-Brent"
print "PI = " + str$(pi) + " <--- Panoramic"

end
rem ============================================================================
' Formule de Leonhard Euler (1707-1783)
' PI² = 6 * (1 + 1/2² + 1/3² + 1/4² + 1/5² ......)
FNC Pi_Euler()
   ' ....
   ' ....
   ' ....
   result quelqueChose
END_FNC
rem ============================================================================
' Développement en série de arctg x avec x = 1
' (W.Leibniz 1646-1716 ou James Gregory 1638- 1675)
' pi = 4 * (1 - 1/3 + 1/5 - 1/7 + 1/9 ......)
FNC Pi_AtnX_1()
   ' ....
   ' ....
   ' ....
   result quelqueChose
END_FNC
rem ============================================================================
' Développement en série de arctg x avec x = sqr(3) / 3 (Euler)
' pi = 2 * sqr(3) * (1 - 1/3 * 1/3¹ + 1/5 * 1/3² - 1/7 * 1/3³ + ...)
FNC Pi_AtnX_SQR3()
   ' ...
   ' ...
   ' ...
   result quelqueChose
END_FNC
rem ============================================================================
' Formule de John Machin (1685-1751) à partir de arctg 1/5 - arctg 1/239
' pi = 16 * (1/5^1 - 1/3 * 1/5^3 + 1/5 * 1/5^5 - 1/7 * 5^7 + ...)
' - 4 * (1/239^1 - 1/3 * 1/239^3 + 1/5 * 1/239^5 - 1/7 * 1/239^7 + ...)
FNC Pi_Machin()
   ' ...
   ' ...
   ' ...
   result quelqueChose
END_FNC
rem ============================================================================
' Formule de John Wallis (1616-1703)
' pi = 2 * (2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * ...)
' Marc
FNC Pi_Wallis()
   DIM_LOCAL dimanche,vacances_scolaires,repos
   vacances_scolaires = 2
   repos = 1
   FOR dimanche = 1 to 5E3 STEP 2
   repos = repos * (vacances_scolaires / dimanche)
   IF dimanche = vacances_scolaires + 1
   vacances_scolaires = vacances_scolaires + 2
   dimanche = dimanche - 2
   END_IF
   NEXT dimanche
   repos = repos * 2
   RESULT repos
END_FNC
rem ============================================================================
' Formule de François Viète (1540-1603)
' 2/pi = sqr(1/2) * sqr(1/2 + 1/2 * sqr(1/2)) * ...
FNC Pi_Viete()
   ' ...
   ' ...
   ' ...
   result quelqueChose
END_FNC
rem ============================================================================
' Formule de Brouncker (1620-1684)
' 4/pi = 1+1²/(2+3²/(2+5²/(2+7²/.....)))
FNC Pi_Brouncker()
   ' ...
   ' ...
   ' ...
   result quelqueChose
END_FNC
rem ============================================================================
' Formule basée sur les moyennes arithmétique et géométrique.
' Formule découverte par Eugène Salamin et Richard Brent en 1976
' a0 = 1 : b0 = 1/sqr(2)
' a(n+1) = (a(n)+ b(n)) / 2 : b(n+1) = sqr(a(n) * b(n))
' Un = 4*a²(n) / (1 - 2 * somme(2^i * (a²(i) - b²(i)))) ; i de 1 = n
' n ---> infini ; Un ---> pi
' ------------------------------------------------------------------------------
' Papydall
FNC Pi_Salamin_Brent()
   dim_local s_carre, puissance2,a,b,an,bn,Un,u,epsilon
   epsilon = 1E-6
   s_carre = 0 : puissance2 = 1 : an = 1 : bn = 1/sqr(2)
   u = 1 : Un = 0
   while not(abs(u-un) < epsilon)
   a = an : b = bn : u = Un
   an = (a+b)/2 : bn = sqr(a*b)
   puissance2 = puissance2 * 2
   s_carre = s_carre + puissance2 * (an*an - bn*bn)
   Un = 4*an*an / (1-2*s_carre)
   end_while
   result Un
END_FNC
rem ============================================================================

Résultat au bout de 5000 itérations:

Bon dimanche à tous !

Bonjour tout le monde.
@Marc
Merci pour ta participation.
J’adore ta façon de nommer les identificateurs, c’est original et plein d’humour, merci. king

Seulement, (il y a toujours un seulement avec Papydall ), le résultat n’est correct qu’à … seulement trois pauvres décimales Sad

PI = 3.14190682856194
PI = 3.14159265358979 d’après Panoramic.

Peut mieux faire ! scratch

Merci quand même.

A+

Eh m'sieur, c'n'est pas ma faute, c'est d'la faute à John !
C'est sa progression qui est trop lente ! lol!

Au risque de me ramasser encore un "peut mieux faire", j'ose une nouvelle approche. C'est comme ça qu'on progresse...
Nouveau calcul pour la suite de Wallis John :

Code:: PRINT Pi_Wallis(5000)
PRINT Pi_Wallis(10000)
PRINT Pi_Wallis(50000)
PRINT Pi_Wallis(100000)
END

FNC Pi_Wallis(n)
   DIM_LOCAL i,x
   x = 1
   FOR i = 2 to n STEP 2
   x = x*(i/(i-1))*(i/(i+1))
   NEXT i
   RESULT x*2
END_FNC

Ce qui donne :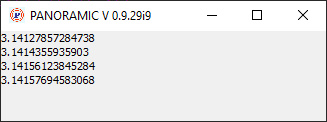

Calcul de PI à l'aide des formules de développement en série 1_bmp49

En augmentant n, la précision sera meilleure mais le temps de calcul sera long, très long...

Marc a écrit:: C'est sa progression qui est trop lente !

Tu as parfaitement raison et bravo d’avoir tenté de relever le challenge.
Jusqu’à nouvel ordre, tu es le champion, à moins qu’un Silverman ou autre Jean comme jean_debord, Jean Claude, Jean le Martien, Jean JL35, Jean Jacques etc, décide(nt) de te détronner.

Voici mon cadeau à toi

Code:: rem ============================================================================
rem Calcul de Pi par la méthode d’Archimède
rem ============================================================================

print str$(Pi_Archimede()) + " <--- Méthode d'Archimède"
print str$(pi) + " <--- Panoramic"
end
rem ============================================================================
' La méthode d’Archimède conduit aux relations de récurence suivantes :
' c <--- sqr((1+c) / 2)
' s <--- s / c
' avec les valeurs initiales C = 0 et S = 2

FNC Pi_Archimede()
   dim_local c,s,t,i
   c = 0 : s = 2
   ' il suffit de 24 itérations pour atteindre 14 décimales justes
   for i = 1 to 24
   c = sqr((1+c)/2) : s = s/c
   next i
   result s
END_FNC
rem ============================================================================

Apprécier la vitesse : l'affichage est instantané !

WAOU !
Trois itérations seulement pour obtenir 13 décimales exactes de PI (la dernière étant arrondie)
Qui dit mieux ?

Code:: rem ============================================================================
rem Calcul de pi par la méthode de Gauss
rem ============================================================================
rem La méthode algorithmique classique est basée sur une étude de Gauss relative
rem à la moyenne arithmético-géométrique de deux nombres.
rem Au lieu d’utiliser une suite infinie, le calcul s’effectue en boucle.
rem Chaque boucle (itération) permet de doubler la quantité de décimales.
rem Après seulement 3 itérations on obtient déjà 13 décimales exactes,
rem la dernière est arrondie.
rem ============================================================================
print : print
print " pi = " + str$(Pi_Gauss()) + " <--- par la méthode de Gauss"
print " pi = " + str$(pi) + " <---- Panoramic"

end
rem ============================================================================
FNC Pi_Gauss()
   dim_local a,b,c,p,x,y,i
   a = 1 : x = 1 : b = 1/sqr(2) : c = 1/4 : ' valeurs initiales
   for i = 1 to 3 : ' 3 itérations suffisent pour obtenir 13 décimales exactes
   y = a
   a =(a+b) / 2
   b = sqr(b*y)
   c = c - x*(a-y)*(a-y)
   x = 2*x
   p = (a+b) * (a+b) / (4*c)
   next i
   result p
END_FNC
rem ============================================================================

Ma réponse est 22/7.

J’aime bien aussi la proposition de

Madhava of Sangamagrama (Inde)
https://pi.ac3j.fr/mot-cle/pi/

Sinon

mateo.over-blog.org/article-un-petit-poeme-pour-retenir-le-nombre-pi-43330552.html

Seul, le premier vers est juste (Après, bonjour les dégâts !)

and

Happy day to everybody :

Depuis, des défenseurs de τ ont créé le Tau day au 28 juin (6/28) en concurrence avec le Pi day du 14 mars (3/14)9
(source:wikipedia)

Ci-après, utilisation bien pratique de la corde à 13 noeuds (qu’on peut aussi lester d’un plomb).
https://xavier.hubaut.info/coursmath/var/13noeuds.htm

Code basé sur la formule de Leonhard Euler:

Code:: rem ============================================================================
rem Calcul de PI par des formules basées sur un développement en série.
rem ============================================================================

font_name 0,"fixedsys" : font_bold 0

print "PI = " + str$(Pi_Euler()) + " <--- Formule Leonhard Euler"
print "PI = " + str$(pi) + " <--- Panoramic"

end
rem ============================================================================
' Formule de Leonhard Euler (1707-1783)
' PI² = 6 * (1 + 1/2² + 1/3² + 1/4² + 1/5² ......)
FNC Pi_Euler()
dim_local i,pi2,k
'
pi2=0
for i=1 to 1000
pi2=pi2+(1/power(i,2))
next i
pi2=pi2*6
k=sqr(pi2)
'
result k
END_FNC
rem ============================================================================

ça ne progresse pas vite! Sad

Merci Silverman pour ta participation.
C’est vrai que la convergence est lente.
J’ai testé une grande quantité de formules d’approximation de Pi.
Je n’ai pas rencontré une méthode meilleure que celle de la moyenne arithmético-géométrique de deux nombres que j’ai postée ci-haut.

» Calcul d’angle ALIAS Question de calcul de moyenne : RESOLU
» a laide pour codé
» Scripts en formules dynamiques
» Reprise du développement
» Les programmes de papydall