| Novembre 2024 | | Lun | Mar | Mer | Jeu | Ven | Sam | Dim |
|---|
| | | | | 1 | 2 | 3 | | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | 11 | 12 | 13 | 14 | 15 | 16 | 17 | | 18 | 19 | 20 | 21 | 22 | 23 | 24 | | 25 | 26 | 27 | 28 | 29 | 30 | |  Calendrier Calendrier |
|
|
| | Rotation d'un rectangle |  |
| | | Auteur | Message |
|---|
JL35
Nombre de messages : 7112
Localisation : 77
Date d'inscription : 29/11/2007
 |  Sujet: Rotation d'un rectangle Sujet: Rotation d'un rectangle  Sam 18 Aoû 2018 - 19:58 Sam 18 Aoû 2018 - 19:58 | |
| C'est tout simple, la rotation se fait autour du centre du rectangle, d'un angle donné. On donne à la sub les coordonnées de l'angle supérieur gauche et les dimensions du rectangle d'origine, et l'angle de rotation en degrés dans le sens des aiguilles. - Code:
-
' Rotation d'un rectangle d'un angle donné
DIM x%,y%,w%,h%,an%
PICTURE 1: FULL_SPACE 1: 2D_TARGET_IS 1
x% = 100: y% = 100: w% = 300: h% = 200
2D_PEN_DOT: 2D_RECTANGLE x%,y%,x%+w%,y%+h%: ' référence, pour voir
an% = 30: ' rotation 30 degrés à droite
2D_PEN_SOLID: 2D_PEN_WIDTH 2
Rectangle_Rot(x%,y%,w%,h%,an%)
END
' ==============================================================================
SUB Rectangle_Rot(x%,y%,w%,h%,an%)
' Rectangle enveloppe en x%,y%, dimensions w%,h%, pivoté de an% degrés
' dans le sens des aiguilles (couleur et épaisseur du trait courants).
DIM_LOCAL r,a%(4),a1%(4),i%,xc%,yc%,x1%,y1%
DEGREES
xc% = x%+w%/2: yc% = y%+h%/2: ' centre de rotation
r = SQR(w%*w%/4 + h%*h%/4)
a%(1) = ATN(h%/w%): a%(2) = 360-a%(1): a%(3) = 180+a%(1): a%(4) = 180-a%(1)
FOR i% = 1 TO 4: a1%(i%)=a%(i%)+an%: NEXT i%
x1% = xc%+r*COS(a1%(1)): y1% = yc%+r*SIN(a1%(1)): 2D_POLY_FROM x1%,y1%
x% = xc%+r*COS(a1%(2)): y% = yc%+r*SIN(a1%(2)): 2D_POLY_TO x%,y%
x% = xc%+r*COS(a1%(3)): y% = yc%+r*SIN(a1%(3)): 2D_POLY_TO x%,y%
x% = xc%+r*COS(a1%(4)): y% = yc%+r*SIN(a1%(4)): 2D_POLY_TO x%,y%
2D_POLY_TO x1%,y1%
END_SUB
' ============================================================================== 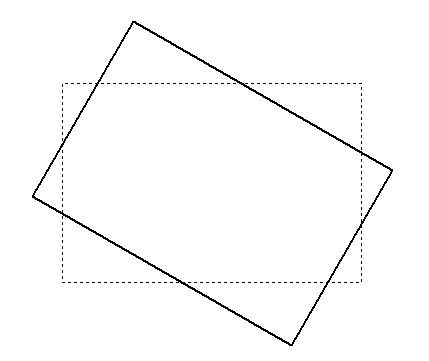 NB la rotation ne concerne que l'enveloppe du rectangle, pas son contenu. | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Rotation d'un rectangle Sujet: Re: Rotation d'un rectangle  Sam 18 Aoû 2018 - 22:54 Sam 18 Aoû 2018 - 22:54 | |
| Salut JL35. Ton rectangle a bien fait sa rotation. Bravo pour les deux (heu ... je vœux dire le rectangle et toi !) Bon, voici une autre approche pour faire tourner à peu près toute figure. Pour incliner une figure il suffit d’appliquer la matrice de rotation à tous les points de la figure. https://panoramic.1fr1.net/t4891-un-cour-incline-une-ellipse-inclinee?highlight=ellipsehttps://panoramic.1fr1.net/t3755-rotation-dune-figure-autour-de-lorigine?highlight=rotationApplication : - Code:
-
rem ============================================================================
rem Rotation d’une figure autour de l’origine
rem par Papydall
rem ============================================================================
dim x0,y0,a,newx,newy, zoom
picture 10 : full_space 10 : 2d_target_is 10
x0 = width(10)/2 : y0 = height(10)/2 : ' Coordonée de l'origine
zoom = 30 : ' facteur d'aggrandissement
Trace_Figure() : ' on trace une figure , une flèche vers le haut comme exemple
' On va tourner cette figure autour de l'origine
for a = 0 to 360 step 10 : ' Faire un tour complet
cls
2d_line 0,y0, 2*x0,y0 : ' tracé de l'axe horizontal
2d_line x0,0, x0,2*y0 : ' tracé de l'axe vertcal
Rotation_Figure(a) : ' Tourner la figure
pause 50
next a
end
rem ============================================================================
' Tracé d'une flèche comme exemple
SUB Trace_Figure()
dim_local i,p,x,y
restore
read p : read x : read y : 2d_poly_from x0 + zoom * x, y0 - zoom * y
for i = 2 to p
read x : read y : 2d_poly_to x0 + zoom * x,y0 - zoom * y
next i
END_SUB
rem ============================================================================
' Rotation de la flèche de l'exemple autour de l'origine des axes d'un angle en degrés
' Pour faire tourner une figure, il suffit de faire tourner tous ses points
SUB Rotation_Figure(angle)
dim_local i,p,x,y
restore
read p : read x : read y : Rotation_Point(x,y,angle)
2d_poly_from x0 + zoom * newx, y0 - zoom * newy
for i = 2 to p
read x : read y : Rotation_Point(x,y,angle)
2d_poly_to x0 + zoom * newx,y0 - zoom * newy
next i
END_SUB
rem ============================================================================
' Rotation autour de l'origine d'un point (x,y) d'un angle tetha en degrés.
' Pour effectuer une rotation à un point il suffit de multiplier ses coordonnées
' par la matrice de rotation suivante :
' cos(tetha) -sin(tetha)
' sin(tetha) cos(tetha)
SUB Rotation_Point(x,y,tetha)
dim_local rad,t
rad = pi/180 : t = rad * tetha
newx = x * cos(t) - y * sin(t)
newy = x * sin(t) + y * cos(t)
END_SUB
rem ============================================================================
' dessin d'une flèche
data 8 : ' nombre de points de la figure
data 3,0 : ' coordonnées 1er point
data 4,0 : ' coordonnées 2ème point
data 4,3
data 5,3
data 3.5,4.5
data 2,3
data 3,3
data 3,0 : ' coordonnées derner point qui est le même que le 1erpour boucler la boucle
rem ============================================================================
- Code:
-
rem ============================================================================
rem Inclinaison d’une figure
rem ============================================================================
rem Pour incliner une figure, il suffit d’appliquer la matrice de rotation à
rem tous les points de la figure.
rem ============================================================================
rem
rem __________________________________________________
rem | |
rem | xp = cx + (x1*cos(IncliDeg) - y1*sin(Inclideg)) |
rem | yp = cy - (x1*sin(IncliDeg) + y1*cos(IncliDeg)) |
rem |__________________________________________________|
rem
rem xp,yp : coordonnées du point à tracer
rem cx,cy : coordonnées du centre de la figure
rem x1,y1 : coordonnées du point avant rotation
rem IncliDeg : valeur de l’angle de rotation (en degré) , sens trigonométrique
rem ============================================================================
rem Application :
rem Tracer une ellipse inclinée
rem Appel : Ellipse_Inclinee(cx,cy,rx,ry,IncliDeg)
2d_pen_color 255,0,0 : Ellipse_Inclinee(300,220,200,100,30)
2d_pen_color 0,0,255 : Ellipse_Inclinee(300,220,200,100,150)
end
rem ============================================================================
' cx,cy : coordonnées du centre de rotation de l'ellipse
' Rx et Ry sont les longueurs des demi-diagonales
' IncliDeg : inclinaison en degrés de l'ellipse dans le sens trigonométrique
SUB Ellipse_Inclinee(cx,cy,rx,ry,IncliDeg)
dim_local a,x1,y1,xp,yp
degrees
IncliDeg = 0-IncliDeg
' Calcul du point Origine
x1 = rx*sin(IncliDeg) : y1 = ry*cos(IncliDeg)
xp = cx + (x1*cos(IncliDeg) - y1*sin(IncliDeg))
yp = cy + (x1*sin(IncliDeg) + y1*cos(IncliDeg))
2d_poly_from xp,yp
for a = 0 to 360
x1 = rx*sin(a + IncliDeg) : y1 = ry*cos(a + IncliDeg)
' Application de la matrice de rotation par rapport au centre cx,cy
xp = cx + (x1*cos(IncliDeg) - y1*sin(IncliDeg))
yp = cy + (x1*sin(IncliDeg) + y1*cos(IncliDeg))
2d_poly_to xp,yp
next a
END_SUB
rem ============================================================================
- Code:
-
rem ============================================================================
rem Inclinaison
rem ============================================================================
Incliner()
end
rem ============================================================================
SUB Incliner()
dim_local a
degrees
for a = 0 to 360 step 30
cls
Coeur_Incline(300,250,100,a)
Ellipse_Inclinee(100,250,100,50,a)
pause 1000
next a
END_SUB
rem ============================================================================
' cx,cy = coordonnées du creux du coeur
' Ro = rayon du coeur
' IncliDeg = inclinaison en degrés du coeur par rapport à la verticale
SUB Coeur_Incline(cx,cy,ro,IncliDeg)
dim_local a,Theta,x1,y1,xp,yp
degrees
2d_pen_width 2
' Calcul du point Origine
x1 = sin(IncliDeg) : x1 = Ro*x1*x1*x1
y1 = cos(IncliDeg) : y1 = Ro*(y1-y1*y1*y1*y1)
xp = cx + (x1*cos(IncliDeg) - y1*sin(Inclideg))
yp = cy - (x1*sin(IncliDeg) + y1*cos(IncliDeg))
2d_poly_from xp,yp
for a = 0 to 360
' Calcul du vecteur du Coeur avec Formule de Raphaël Laporte
Theta = a + IncliDeg
x1 = sin(Theta) : x1 = Ro*x1*x1*x1
y1 = cos(Theta) : y1 = Ro*(y1-y1*y1*y1*y1)
' Application de la matrice de rotation par rapport au centre cx,cy
xp = cx + (x1*cos(IncliDeg) - y1*sin(Inclideg))
yp = cy - (x1*sin(IncliDeg) + y1*cos(IncliDeg))
2d_poly_to xp,yp
next a
END_SUB
rem ============================================================================
' cx,cy : coordonnées du centre de rotation de l'ellipse
' Rx et Ry sont les longueurs des demi-diagonales
' IncliDeg : inclinaison en degrés de l'ellipse par rapport à la verticale
SUB Ellipse_Inclinee(cx,cy,rx,ry,IncliDeg)
dim_local a,x1,y1,xp,yp
degrees
2d_pen_width 2
' Calcul du point Origine
x1 = rx*sin(IncliDeg) : y1 = ry*cos(IncliDeg)
xp = cx + (x1*cos(IncliDeg) - y1*sin(IncliDeg))
yp = cy + (x1*sin(IncliDeg) + y1*cos(IncliDeg))
2d_poly_from xp,yp
for a = 0 to 360
x1 = rx*sin(a + IncliDeg) : y1 = ry*cos(a + IncliDeg)
' Application de la matrice de rotation par rapport au centre cx,cy
xp = cx + (x1*cos(IncliDeg) - y1*sin(IncliDeg))
yp = cy + (x1*sin(IncliDeg) + y1*cos(IncliDeg))
2d_poly_to xp,yp
next a
END_SUB
rem ============================================================================
| |
|   | | JL35
Nombre de messages : 7112
Localisation : 77
Date d'inscription : 29/11/2007
 |  Sujet: Re: Rotation d'un rectangle Sujet: Re: Rotation d'un rectangle  Sam 18 Aoû 2018 - 23:10 Sam 18 Aoû 2018 - 23:10 | |
| Bonsoir papydall, Effectivement j'ai fait au plus simple (simpliste ?) mais il me semblait bien que tu avais une solution bien plus universelle... (je cherchais notamment la rotation d'ellipse...) Je note soigneusement tout ça, et merci à toi. Je vais maintenant m'attaquer à la rotation du cercle  | |
|   | | JL35
Nombre de messages : 7112
Localisation : 77
Date d'inscription : 29/11/2007
 |  Sujet: Re: Rotation d'un rectangle Sujet: Re: Rotation d'un rectangle  Sam 18 Aoû 2018 - 23:12 Sam 18 Aoû 2018 - 23:12 | |
| | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Rotation d'un rectangle Sujet: Re: Rotation d'un rectangle  | |
| |
|   | | | | Rotation d'un rectangle |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
