| Novembre 2024 | | Lun | Mar | Mer | Jeu | Ven | Sam | Dim |
|---|
| | | | | 1 | 2 | 3 | | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | 11 | 12 | 13 | 14 | 15 | 16 | 17 | | 18 | 19 | 20 | 21 | 22 | 23 | 24 | | 25 | 26 | 27 | 28 | 29 | 30 | |  Calendrier Calendrier |
|
|
| | Appel aux matheux |  |
| | | Auteur | Message |
|---|
Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Appel aux matheux Sujet: Appel aux matheux  Mar 11 Aoû 2015 - 16:04 Mar 11 Aoû 2015 - 16:04 | |
| Je ne m'y retrouve plus dans mes sinus ...
J'ai besoin de vous, les formules de math se chamboulent dans ma tête ...
Si j'ai deux points A et B avec des coordonnées connues Xa, Ya et Xb,Yb
J'ai un autre point: O dont j'ai les coordonnées (Xo,Yo) pour être original ...
Je ne sais plus comment on obtient l'angle AOB.
Je sais que c'est simple, mais je ne retrouve pas. Pire, en cherchant sur google, je me suis fait mal à la tête mais je n'ai pas trouvé ... alors plutôt que de m'auto flageller, j'en appelle à vous pour qui cela coule de source ... | |
|   | | Yannick
Nombre de messages : 8635
Age : 53
Localisation : Bretagne
Date d'inscription : 15/02/2010
 |  Sujet: re Sujet: re  Mar 11 Aoû 2015 - 21:11 Mar 11 Aoû 2015 - 21:11 | |
| | |
|   | | Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mar 11 Aoû 2015 - 22:20 Mar 11 Aoû 2015 - 22:20 | |
| Non mais je t'explique, les maths, c'est top loin. A partir des coordonnées des 3 points, ma pauve petite tête ne se souveint plus comment faire ... Bon en plus c'était mon anniversaire, alors après l'apéro, le vin rouge et le mousseux, tu penses bien que je n'y capte rien ... Si quelqu'un peut traduire en matho resistant, ça serait cool. | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mar 11 Aoû 2015 - 22:28 Mar 11 Aoû 2015 - 22:28 | |
| Joyeux anniversaire Jicehel. Le mien était hier (un jour avant toi !). La formule d’Al-Kashi peut résoudre ton problème. Dans quelques instants je te mâcherai le travail comme cadeau pour ton anniversaire.  | |
|   | | Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mar 11 Aoû 2015 - 22:44 Mar 11 Aoû 2015 - 22:44 | |
| Merci Papydall et bon anniversaire à toi en retard d'une journée avec toute mes excuses pour le retard | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mar 11 Aoû 2015 - 23:00 Mar 11 Aoû 2015 - 23:00 | |
| On connait les coordonnées de trois points A(xa,ya) ; B(xb,yb) ; C(xc,yc) Ces trois points forment un triangle quelconque. On calcule les longueurs des trois côtés du triangle (a,b,c) respectivement opposés aux angles A,B,C La Formule d’Al-Kashi : a² = b² + c² -2bcCos(A) a,b,c sont respectivement les côtés opposées aux angles A,B,C. De la formule d’Al-Kashi on tire : A = acos( (b²+c²-a²)/(2bc)) La valeur calculée est en radians, pour obtenir l’angle en degrés, il suffit de multiplier par 180/pi - Code:
-
rem ============================================================================
rem Formule d Al-Kashi dans un triangle quelconque
rem ============================================================================
' a² = b² + c² -2bcCos(A)
' 2bcCos(A) = b² +c² -a²
' Cos(A) = (b²+c²-a²)/(2bc)
' A = acos( (b²+c²-a²)/(2bc))
rem ============================================================================
dim xa,ya,xb,yb,xo,yo : ' coordonnées des points A,B,O
dim a,b,c : ' longueures des côtés (du triangle) opposées à A,B,O
dim longueur : ' longueur d'un côté du triangle
dim angle : ' angle du triangle
dim pi : pi = acos(-1)
rem Exemple 1:
' xa = 1 : ya = 1
' xb = 1 : yb = 0
' xo = 0 : yo = 0
rem Exemple 2
xa = 2 : ya = -3
xb = 3 : yb = 1
xo = -1 : yo = 4
' On détermine les mesures des trois côtés du triangle
Longueur_Cote(xo,yo,xa,ya) : b = longueur : print "Longueur du côté b = " + str$(b)
Longueur_Cote(xo,yo,xb,yb) : a = longueur : print "Longueur du côté a = " + str$(a)
Longueur_Cote(xa,ya,xb,yb) : c = longueur : print "Longueur du côté c = " + str$(c)
' On détermine la valeur de l'angle AOB
Angle_A(a,b,c) : print "L'angle AOB = " + str$(angle) + " radians, soit : " + str$(angle*180/pi) + "°"
end
rem ============================================================================
' Déterminer la longueur d'un segment délimité par deux points dont les
' coordonnées sont x1,y1 et x2,y2
SUB Longueur_Cote(x1,y1,x2,y2)
longueur = sqr((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1))
END_SUB
rem ============================================================================
' Déterminer l'angle A (en radians) en utilisant la formule d'Al-Hashi
SUB Angle_A(a,b,c)
dim_local a2,b2,c2
a2 = a*a : b2 = b*b : c2 = c*c
angle = acos((b2+c2-a2)/(2*b*c))
END_SUB
rem ============================================================================
Il va sans dire (mais il va mieux en le disant) que je répondrai toujours présent à toute demande dans les limites de mes compétences.  Code édité pour correction d'une erreur de codage. Code édité pour correction d'une erreur de codage.Re EDIT A,B,C représentent les angles du triangle a,b,c représentent les côtés opposés à A,B,C Le théorème d’El-Kashi donne les formules suivantes pour le calcul des trois angles d’un triangle connaissant les mesures des trois côtés de ce même triangle. A = acos((b²+c²-a²)/(2*b*c)) B = acos((c²+a²-b²)/(2*c*a)) C = acos((a²+b²-c²)/(2*a*b)) | |
|   | | Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mer 12 Aoû 2015 - 1:02 Mer 12 Aoû 2015 - 1:02 | |
| Merci Papydall, bon mon programme pour voir si un point et dans un polygone ne marche quand même pas. J'ai encore dû rater un truc mais je finirais bien par trouver ... En tout cas, merci pour ton aide plus efficace que mon meilleur ami: Google  | |
|   | | Klaus

Nombre de messages : 12331
Age : 75
Localisation : Ile de France
Date d'inscription : 29/12/2009
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mer 12 Aoû 2015 - 1:43 Mer 12 Aoû 2015 - 1:43 | |
| Une technique simple pour résoudre ce problème, quoique certainement pas optimisée: 1. soit P=[p1,p2,...,pn] un polygone avec n sommets p1 à pn 2. soit z un point quelconque 3. déterminer les côtés du polygone P qui "englobent" l'ordonnée du point z 4. compter le nombre de côtés "à gauche" du point z, et le nombre de côtés à droite du point z 5. si ces deux nombres sont impairs, le point z est dans le polygone. Sinon, il est dehors. Petite illustration, tracée à main levée avec PAINT: 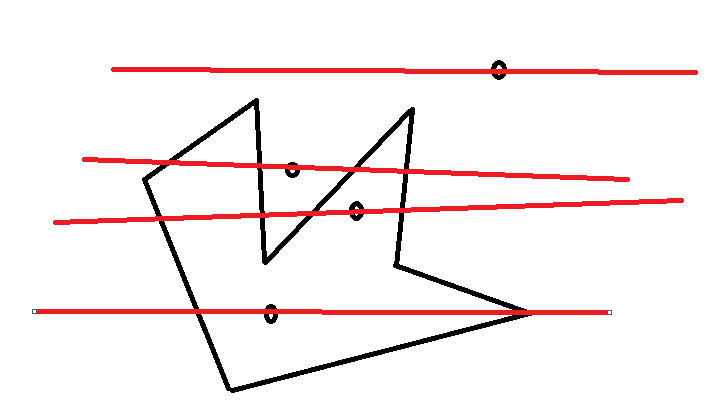 Sachant qu'un côté du polygone est le segment [pi,pi+1[ (oui, ici on exclut le point terminal, pour gérer le cas où le point z serait exactement à la hauteur d'un coin du polygone P). Sachant qu'on détermine si un point est à gauche ou à droite du point z en calculant l'abscisse d'un point y située sur la droite passant par le segment et ayant la même abscisse que le point z. Voilà. Il n'y a plus qu'à coder. Et le point fort de cet algorithme est qu'il marche même si les côtés du polygone se chevauchent ! | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mer 12 Aoû 2015 - 4:37 Mer 12 Aoû 2015 - 4:37 | |
| Voici mon second cadeau à Jicehel. Les autres aussi peuvent en profiter !  - Code:
-
rem ============================================================================
rem teste si un point X,Y est à l interieur d un polygone
rem rem ========================================================================
dim Nbpoint : NbPoint = 12 : ' nombre de sommets du polygone
dim MatXY(NbPoint,2) : ' matrice contenant les coordonnées X,Y des sommets du polygone
dim InRegion : ' Variable de retour de la SUB/FONCTION InRegion(x,y)
' Si le point se trouve dans la région, InRegion vaut 1
' Si le point se trouve sur la frontière, InRegion vaut -1
' Si le point se trouve en dehors de la région, InRegion vaut 0
dim i : ' variable compteur
' définition de la matrice du polygone
MatXY(0,1) = 200 : MatXY(0,2) = 340
MatXY(1,1) = 200 : MatXY(1,2) = 240
MatXY(2,1) = 240 : MatXY(2,2) = 240
MatXY(3,1) = 320 : MatXY(3,2) = 140
MatXY(4,1) = 200 : MatXY(4,2) = 220
MatXY(5,1) = 260 : MatXY(5,2) = 080
MatXY(6,1) = 200 : MatXY(6,2) = 100
MatXY(7,1) = 180 : MatXY(7,2) = 080
MatXY(8,1) = 120 : MatXY(8,2) = 100
MatXY(9,1) = 020 : MatXY(9,2) = 060
MatXY(10,1) = 010 : MatXY(10,2) = 400
MatXY(11,1) = 100 : MatXY(11,2) = 340
MatXY(12,1) = 200 : MatXY(12,2) = 340
' Tracé du polygone
2d_poly_from MatXY(0,1),MatXY(0,2)
for i = 1 to NbPoint : 2d_poly_to MatXY(i,1),MatXY(i,2) : next i
' Appels à la SUB/FONCTION InRegion(x,y)
InRegion(200,340) : message Inregion : ' Valeur -1 : sur la frontière
InRegion(150,340) : message Inregion : ' Valeur -1 : sur la frontière
InRegion(020,050) : message Inregion : ' Valeur 0 : à l'exterieur de la region
InRegion(100,100) : message Inregion : ' Valeur 1 : à l'interieur de la region
InRegion(240,220) : message Inregion : ' Valeur 1 : à l'interieur de la region
InRegion(240,180) : message Inregion : ' Valeur 0 : à l'exterieur de la region
end
rem ============================================================================
' Renvoie 1 si le point de coordonnées (X,Y) se trouve dans la Région fermée définie par MatXY
' Renvoie 0 si extérieur à la région
' Renvoie -1 si sur la frontière
SUB InRegion(x,y)
dim_local x1,x2,x3,y1,y2,d,i,nb
2d_fill_on : 2d_fill_color 255,0,0 : 2d_circle x,y,5
for i = 0 to NbPoint - 1
x1 = MatXY(i,1) : y1 = MatXY(i,2)
x2 = MatXY(i+1,1) : y2 = MatXY(i+1,2)
' Le point se trouve-t-il sur un segment vertical ?
If ((X1 = X2) And (X1 = X)) And ((Y1 >= Y And Y < Y2) Or (Y1 <= Y And Y > Y2))
InRegion = -1 : exit_sub
End_If
' Le point se trouve-t-il entre le segment [(X1,Y1);(X2,Y2)[ ?
If (X1 <= X And X < X2) Or (X1 >= X And X > X2)
' Calcul distance entre le segment et le point
D = Y - Y1 + (Y1 - Y2) * (X1 - X) / (X1 - X2)
' Test distance D
If D = 0 : ' Sur frontière
InRegion = -1 : exit_sub
Else
If D > 0 : ' le point coupe le segment
nb = nb + 1
If X = X1 : ' à l'aplomb du départ d'un segment
X3 = MatXY(i-1,1)
If i = 1 Then X3 = MatXY(NbPoint,1)
If (X3 < X And X2 < X) Or (X3 > X And X2 > X) Then nb = nb + 1
end_if
End_If
End_If
end_if
Next i
InRegion = odd(nb)
END_SUB
rem ============================================================================
| |
|   | | Minibug

Nombre de messages : 4570
Age : 58
Localisation : Vienne (86)
Date d'inscription : 09/02/2012
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mer 12 Aoû 2015 - 7:20 Mer 12 Aoû 2015 - 7:20 | |
| Salut tout le monde !  Effectivement Papydall, vu sous cet angle (hihihi !), ça parait simple... Ce code est en tous cas très efficace et très rapide. Bravo Papydall ! | |
|   | | Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mer 12 Aoû 2015 - 8:57 Mer 12 Aoû 2015 - 8:57 | |
| Oui, j'avais vu cette méthode sur un forum anglais mais je n'avais pas tout compris dans les explications alors j'ai essayé la méthode de la somme des angles, mais je devais sans doute faire un mélange de degrés et de radians en tout cas ça ne marchait pas. J'ai donc repris la méthode (on peut même dire la procédure toute prête de Papydall pour remplacer celle qui ne fonctionnait pas chez moi. Les points rouges sont en dehors du polygone, les point bleus sur la frontière et les verts à l'intérieur. - Code:
-
DIM Nb_points : Nb_points = 6
DIM Polygone(Nb_points,1) : ' Tableau contenant les 6 couples de points du polygne
DIM Max_x, Max_y : ' Valeurs maximales pour le calcul du zoom
DIM Min_x, Min_y
DIM i%, ind%
DIM Zoom_x, Zoom_y
DIM Bandeau%, Bord%
DIM Collision_Point_Polygone%
DIM Xo, Yo
DIM Collision_Point_AABB_resultat%
DATA 1,4,2,1,3,2,4,1,4,3,7,5
ind% = 1
Retourne_Dimension_Bandeau_Et_Bord()
Max_x = -99999 : Max_y = -99999 : Min_x=99999 : Min_y=99999
FOR i% = 0 TO Nb_points-1
READ Polygone(i%,0) : IF Polygone(i%,0)> Max_x then Max_x = Polygone(i%,0)
IF Polygone(i%,0)< Min_x then Min_x = Polygone(i%,0) : ind% = i%
READ Polygone(i%,1) : IF Polygone(i%,1) > Max_y then Max_y = Polygone(i%,1)
IF Polygone(i%,1)< Min_y then Min_y = Polygone(i%,1)
NEXT i%
Polygone(Nb_points,0) = Polygone(0,0) : Polygone(Nb_points,1) = Polygone(0,1)
PICTURE 1 : WIDTH 1,WIDTH(0) - 2 * Bord% :HEIGHT 1, HEIGHT(0) - Bord% - Bandeau%
Zoom_x = WIDTH(1) / (Max_x + 2) : Zoom_y = HEIGHT(1) / (Max_y+ 2)
2D_TARGET_IS 1
2D_POLY_FROM Polygone(0,0)*Zoom_x,Polygone(0,1)*Zoom_y
FOR i% = 0 TO Nb_points
2D_POLY_TO Polygone(i%,0)*Zoom_x,Polygone(i%,1)*Zoom_y
NEXT i%
Test_Point(2,3) : Test_Point(0,0) : Test_Point(2,1)
Test_Point(1,4) : Test_Point(3,3) : Test_Point(6,3)
Test_Point(1,1) : Test_Point(1,4) : Test_Point(8,1)
Test_Point(3,4) : Test_Point(5,4) : Test_Point(6,6)
Test_Point(3,2) : Test_Point(4,1) : Test_Point(7,5)
END
REM ' ============================================================================
REM ' Merci Papydall pour les formules ;)
REM ' ============================================================================
SUB Collision_Point_Polygone(X%,Y%)
REM ' ============================================================================
REM ' Renvoie 1 si le point de coordonnées (X,Y) se trouve dans la Région fermée définie par MatXY
REM ' Renvoie 0 si extérieur à la région
REM ' Renvoie -1 si sur la frontière
DIM_LOCAL Compte%, X1,X2,X3,Y1,Y2,D
IF X% < Min_x OR X% > Max_x OR Y% < Min_y OR Y% > Max_y THEN Collision_Point_Polygone% = 0 : EXIT_SUB
FOR i% = 0 TO Nb_points -1
X1 = Polygone(i%,0) : Y1 = Polygone(i%,1)
X2 = Polygone(i%+1,0) : Y2 = Polygone(i%+1,1)
' Le point se trouve-t-il sur un segment vertical ?
IF ((X1 = X2) AND (X1 = X%)) AND ((Y1 >= Y% AND Y% < Y2) OR (Y1 <= Y% AND Y% > Y2)) THEN Collision_Point_Polygone% = -1 : EXIT_SUB
' Le point se trouve-t-il entre le segment [(X1,Y1);(X2,Y2)[ ?
IF (X1 <= X% AND X% < X2) OR (X1 >= X% AND X% > X2)
' Calcul distance entre le segment et le point
D = Y% - Y1 + (Y1 - Y2) * (X1 - X%) / (X1 - X2)
' Test distance D
IF D = 0 : ' Sur frontière
Collision_Point_Polygone% = -1 : EXIT_SUB
ELSE
IF D > 0 : ' le point coupe le segment
Compte% = Compte% + 1
IF X% = X1 : ' à l'aplomb du départ d'un segment
X3 = Polygone(i%-1,0)
IF i% = 1 THEN X3 = Polygone(Nb_Points,0)
IF (X3 < X% AND X2 < X%) OR (X3 > X% AND X2 > X%) THEN Compte% = Compte% + 1
END_IF
END_IF
END_IF
END_IF
NEXT i%
Collision_Point_Polygone% = ODD(Compte%)
END_SUB
REM ' ============================================================================
REM ' Cette procédure crée et retourne les variables globales => bandeau% et bord%
REM ' ============================================================================
SUB Retourne_Dimension_Bandeau_Et_Bord()
REM ' Controle de la position de la procédure dans le programme
IF NUMBER_OBJECTS>0
MESSAGE "La SUB 'Retourne_Dimension_Bandeau_Et_Bord' doit être placée avant la création du premier objet !"
TERMINATE
END_IF
REM ' création des VARIABLES GLOBALES
IF VARIABLE("bandeau%")=0 then DIM Bandeau%
IF VARIABLE("bord%")=0 then DIM Bord%
' Calcul de bandeau% et bord%
DIM_LOCAL w0%,h0%,w1%,h1%,w2%,h2%
w0%=WIDTH(0) : h0%=HEIGHT(0)
PICTURE 1 : FULL_SPACE 1 : w1%=WIDTH(1) : h1%=HEIGHT(1)
w2%=w0%-w1% : h2%=h0%-h1%
Bord%=w2%/2
Bandeau%=h2% - Bord%
REM ' Suppression du Picture devenu inutile
DELETE 1
END_SUB
REM ' ============================================================================
REM ' Cette procédure crée et retourne les variables globales => bandeau% et bord%
REM ' ============================================================================
SUB Affiche(Resultat%,Xc%,Yc%)
IF Resultat% = -1 THEN 2D_FILL_COLOR 0,0,255
IF Resultat% = 0 THEN 2D_FILL_COLOR 255,0,0
IF Resultat% = 1 THEN 2D_FILL_COLOR 0,255,0
2D_CIRCLE Xc%*Zoom_x,Yc%*Zoom_y, 5
END_SUB
REM ' ============================================================================
REM ' Cette procédure vérifie si un point est dans un rectangle de type AABB
REM ' Le résultat se retrouve dans la variable Collision_Point_AABB_resultat%
REM ' retourne 0 si le point est en dehors
REM ' retourne 1 si le point est dedans
REM ' ============================================================================
SUB Collision_Point_AABB(point_x%,point_y%,rect_x%,rect_y%,rect_width,rect_height)
Collision_Point_AABB_resultat% = 0
IF rect_x% <= point_x% AND point_x% < rect_x% + rect_width
IF rect_y% <= point_y% AND point_y% < rect_y% + rect_height
Collision_Point_AABB_resultat% = 1
END_IF
END_IF
END_SUB
REM ' ============================================================================
REM ' Procédure de mise en application du test d'un point
REM ' ============================================================================
SUB Test_Point(Xp,Yp)
Collision_Point_AABB(Xp,Yp,Min_x,Min_y,Max_x,Max_y)
IF Collision_Point_AABB_resultat% = 0
Collision_Point_Polygone% = 0
ELSE
Collision_Point_Polygone(Xp,Yp)
END_IF
Affiche(Collision_Point_Polygone%,Xp,Yp)
DISPLAY
END_SUB | |
|   | | Klaus

Nombre de messages : 12331
Age : 75
Localisation : Ile de France
Date d'inscription : 29/12/2009
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mer 12 Aoû 2015 - 10:33 Mer 12 Aoû 2015 - 10:33 | |
| Le 21/12/2014, j'ai publié ceci: - Code:
-
' test_point_dans_polygone.bas
label add, del, test, eff, padd, pdel, ptest, verif
dim ptest%(1), polygon%(100,1), npoints%, x%, y%, s$, i%, j%
dim x1%,x2%, y1%, y2%, yp, nhaut%, nbas%, ferme%
full_space 0 : caption 0,"Verifier si un point est dans un polygone"
picture 1 : full_space 1 : height 1,height(1) - 100 : top 1,100
button 2 : top 2,10 : left 2,10 : caption 2,"Ajouter un point"
width 2,100 : on_click 2,add
button 3 : top 3,40 : left 3,10 : caption 3,"Enlever un point"
width 3,100 : on_click 3,del
button 31 : top 31,70 : left 31,10 : caption 31,"Effacer tout"
width 31,100 : on_click 31,eff
memo 12 : top 12,10 : left 12,300 : width 12,width(0)-360 : bar_both 12
height 12,80
button 4 : top 4,10 : left 4,150 : caption 4,"Point à tester"
width 4,100 : on_click 4,test
alpha 14 : top 14,40 : left 14,150
button 5 : top 5,70 : left 5,150 : caption 5,"Vérifier"
width 5,100 : on_click 5,verif
2d_target_is 1
end
add:
off_click 1
on_click 1,padd
return
del:
off_click 1
on_click 1,pdel
return
test:
off_click 1
on_click 1,ptest
return
eff:
npoints% = 0
ptest%(0) = -1
ptest%(1) = -1
2d_clear
clear 12
caption 14,""
off_click 1
return
padd:
if npoints%=100
message "Trops de points !"
return
end_if
if ferme%=1
2d_pen_color 255,255,255
2d_poly_from polygon%(npoints%,0),polygon%(npoints%,1)
2d_poly_to polygon%(1,0),polygon%(1,1)
2d_pen_color 0,0,0
ferme% = 0
end_if
x% = mouse_x_left_down(1)
y% = mouse_y_left_down(1)
s$ = "("+str$(x%)+","+str$(y%)+")"
if count(12)>0
s$ = item_read$(12,1)+","+s$
clear 12
end_if
item_add 12,s$
npoints% = npoints% + 1
polygon%(npoints%,0) = x%
polygon%(npoints%,1) = y%
if npoints%=1
2d_point x%,y%
else
2d_poly_from polygon%(npoints%-1,0),polygon%(npoints%-1,1)
2d_poly_to x%,y%
end_if
2d_circle x%,y%,3
return
pdel:
if npoints%=0 then return
x% = mouse_x_left_down(1)
y% = mouse_y_left_down(1)
for i%=1 to npoints%
if abs(polygon%(i%,0)-x%)<5
if abs(polygon%(i%,1)-y%)<5
if i%<npoints%
for j%=i% to npoints%
polygon%(j%,0) = polygon%(j%+1,0)
polygon%(j%,1) = polygon%(j%+1,1)
next j%
end_if
npoints% = npoints% - 1
2d_clear
if npoints%>0
2d_circle polygon%(1,0),polygon%(1,1),3
if npoints%>1
for j%=1 to npoints%-1
2d_poly_from polygon%(j%,0),polygon%(j%,1)
2d_poly_to polygon%(j%+1,0),polygon%(j%+1,1)
2d_circle polygon%(j%+1,0),polygon%(j%+1,1),3
next j%
end_if
end_if
if ptest%(0)>=0
2d_fill_color 0,0,255
2d_fill_on
2d_circle ptest%(0),ptest%(1),3
2d_fill_off
2d_fill_color 255,255,255
end_if
end_if
end_if
next i%
return
ptest:
x% = mouse_x_left_down(1)
y% = mouse_y_left_down(1)
s$ = "("+str$(x%)+","+str$(y%)+")"
caption 14,s$
if ptest%(0)>=0
2d_pen_color 255,255,255
2d_fill_on
2d_circle ptest%(0),ptest%(1),3
2d_fill_off
2d_pen_color 0,0,0
end_if
ptest%(0) = x%
ptest%(1) = y%
2d_fill_color 0,0,255
2d_fill_on
2d_circle x%,y%,3
2d_fill_off
2d_fill_color 255,255,255
return
verif:
' le point est "dedans" si une ligne horizontale ou verticale
' passant par le point coupe un nombre impair de segments du polygone.
' formule du segment: yp=((y2-y1)/(x2-x1))*(xp-x1)+y1
' formule de la droite par le point à tester: x = xp
' il faut tester si min(y1,y2)<=yp<=max(y1,y2)
' si oui, la droite verticale par le point coupe le segment
if ptest%(0)<0 then return
if npoints%<3 then return
nhaut% = 0
nbas% = 0
x% = ptest%(0)
y% = ptest%(1)
2d_pen_color 255,0,0
2d_poly_from polygon%(npoints%,0),polygon%(npoints%,1)
2d_poly_to polygon%(1,0),polygon%(1,1)
2d_pen_color 0,0,0
ferme% = 1
for i%=1 to npoints%
x1% = polygon%(i%,0)
y1% = polygon%(i%,1)
if i%<npoints%
x2% = polygon%(i%+1,0)
y2% = polygon%(i%+1,1)
else
x1% = polygon%(1,0)
y1% = polygon%(1,1)
end_if
if min(x1%,x2%)<=x%
if x%<=max(x1%,x2%)
yp = ((y2%-y1%)/(x2%-x1%))*(x%-x1%)+y1%
if min(y1%,y2%)<=yp
if yp<=max(y1%,y2%)
' message "segment "+str$(i%)+" est coupé."
if yp>=y%
nhaut% = nhaut%+1
else
nbas% = nbas% + 1
end_if
end_if
end_if
end_if
end_if
next i%
' message "haut: "+str$(nhaut%)+" bas: "+str$(nbas%)
if odd(nhaut%)=1
message "Le point à tester est à l'intérieur du polygone !"
else
message "Le point à tester est à l'extérieur du polygone !"
end_if
return
| |
|   | | Yannick
Nombre de messages : 8635
Age : 53
Localisation : Bretagne
Date d'inscription : 15/02/2010
 |  Sujet: re Sujet: re  Mer 12 Aoû 2015 - 11:14 Mer 12 Aoû 2015 - 11:14 | |
| Avec un peu de retard mais un bon anniversaire à vous deux (Jicehel et Papydall) .  | |
|   | | Jicehel

Nombre de messages : 5947
Age : 52
Localisation : 77500
Date d'inscription : 18/04/2011
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mer 12 Aoû 2015 - 12:45 Mer 12 Aoû 2015 - 12:45 | |
| Merci Ygeronimi Merci Papydall dont j'ai repris la procédure Merci Klaus, désolé, j'avais raté ton message d'hier. Je ne me souvenais pas de ton programme, mais en effet, c'est le même principe. Du coup, c'es pratique, je vais pouvoir partir de ton explication pour l'article  Du coup je pourrais aborder la suite de ton programme dans l'article aussi  Ca fera déjà de quoi faire pour l'article et dans le suivant j'essayerais de trouver des choses sur l'optimisation des détections par zonage en englobage. | |
|   | | papydall

Nombre de messages : 7017
Age : 74
Localisation : Moknine (Tunisie) Entre la chaise et le clavier
Date d'inscription : 03/03/2012
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  Mer 12 Aoû 2015 - 12:55 Mer 12 Aoû 2015 - 12:55 | |
| Salut tout le monde et merci pour le partage.  | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Appel aux matheux Sujet: Re: Appel aux matheux  | |
| |
|   | | | | Appel aux matheux |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
